1. Rappel des formules fondamentales
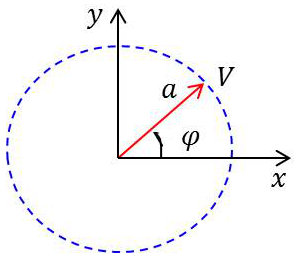 On sait que le mouvement est associé à la projection d’un vecteur tournant avec une vitesse uniforme autour de son origine.
On sait que le mouvement est associé à la projection d’un vecteur tournant avec une vitesse uniforme autour de son origine.
Nous rappelons les formules classiques.
L’équation du mouvement (projection sur l’axe des ordonnées par exemple) est donnée par : \[y=a~\sin(\omega~t+\varphi)\]
\(a\) : amplitude\(\quad;\quad\varphi\) : phase / origine\(\quad;\quad\omega\) : pulsation
\(T\) : période\(\quad;\qquad\nu=\cfrac{1}{T}\) : fréquance\(\quad;\quad~\omega~T=2\pi\)
Les relations des fonctions circulaires aux exponentielles complexes permettent d’introduire le signal sous la forme complexe :
\[\begin{aligned} &z(t)=a~\exp\{j~(\omega~t-\varphi)\}\qquad\text{donc :}\quad y=\mathcal{R}(z)\\ &z(t)=A~\exp(j~\omega~t)\qquad\text{avec :}\quad A=a~\exp(-j~\varphi)\end{aligned}\]
1.1. Oscillateur harmonique
Considérant la forme pure : \[(1)\qquad x=a~\cos(\omega~t+\varphi)\]
Une première dérivation par rapport à t : \[(2)\qquad x'=-a~\omega~\sin(\omega~t+\varphi)\]
Une deuxième dérivation par rapport à t : \[(3)\qquad x''=-a~\omega^2~\cos(\omega~t+\varphi)\]
En additionnant membre à membre les relations (1) et (2) : \[(4)\qquad x''+\omega^2~x=0\]
On reconnaît l(équation classique du mouvement pendulaire parfait (sans pertes de frottements)
1.2. Caractéristique énergétique
Nous raisonnerons par analogie en reprenant l’exemple du mouvement de la masse \(m\) attachée à un ressort de raideur (constante de rappel \(k\)) : \[\overrightarrow{f}=m~\overrightarrow{\gamma}\qquad\Rightarrow\qquad m~x''=-k~x\quad;\quad x''+\frac{k}{m}~x=0\]
D’où : \[\omega=\sqrt{\frac{k}{m}}\quad;\quad T=2~\pi~\sqrt{\frac{m}{k}}\]
Expression des énergies (cinétique, potentielle et mécanique totale) : \[\left\{ \begin{aligned} &E_c=\frac{1}{2}~m~x'^2\\ &E_p=\frac{1}{2}~k~x^2\\ &E_m=E_p+E_c=\frac{1}{2}~k~a^2 \end{aligned} \right.\]
On voit que l’énergie de la vibration est proportionnelle au carré de l’amplitude de cette vibration.
2. Composition de mouvements vibratoires de même période
On considère les deux mouvements : \[\left\{ \begin{aligned} z_1=a_1~e^{-j~\varphi_1}~e^{j~\omega~t}=A_1~e^{j~\omega~t}\\ z_2=a_2~e^{-j~\varphi_2}e^{j~\omega~t}=A_2~e^{j~\omega~t} \end{aligned} \right. \quad\rightarrow\quad z=z_1+z_2=(A_1+A_2)~e^{j~\omega~t}\]
Le mouvement résultant est un mouvement sinusoïdal, de même pulsation que les mouvements composants et dont l’amplitude complexe est la somme des deux amplitudes complexes : \[A=A_1+A_2=a_1e^{-j~\varphi_1}+a_2~e^{-j~\varphi_2}\]
Calcul de l’amplitude complexe résultante
Un calcul élémentaire conduit à la relation : \[a^2=A~A^*=a_1^2+a_2^2+2~a_1~a_2~\cos(\varphi_1-\varphi_2)\]
Quant au terme de déphasage, il peut se déduire de : \[A=a_1~(\cos\varphi_1-j~\sin\varphi_1)+a_2~(\cos\varphi_2-j~\sin\varphi_2)\]
C’est-à-dire : \[\tan\varphi=\frac{a_1~\sin\varphi_1+a_2~\sin\varphi_2}{a_1~\cos\varphi_1+a_2~\cos\varphi_2}\]
3. Problème de la cohérence
En pratique, aucune source ne peut vibrer de façon continue de \(t=-\infty\) à \(t=+\infty\), car il y a toujours amortissement et il faut relancer la vibration par un nouvel apport d’énergie. L’oscillateur reprend à chaque fois un mouvement de même période, mais qui doit être considéré comme indépendant du précédent car phase et amplitude ont changé brusquement.
L’intervalle de temps \(\Delta t=n~T\gg T\) pendant lequel on peut admettre que la vibration n’est pas perturbée est appelé temps de cohérence. On admet que : \[a^2=\frac{A_1~A_1^*+A_2~A_2^*+\dots+A_n~A_n^*}{n}\]
Si donc nous considérons deux sources différentes ou deux points différents d’une même source, les variations brusques de \(A\) et \(\varphi\) se produisent à des instants différents et y ont des valeurs sans relation entre elles. Ces deux points constituent des sources incohérentes et les vibrations qu’elles envoient sont des vibrations incohérentes.
3.1. Composition de deux vibrations incohérentes
Soient \(s_1\) et \(s_2\) les deux vibrations. L’énergie qui en résulte est : \[\overline{A~A^*}=\overline{a_1^2}+\overline{a_2^2}+2~\overline{a_1}~\overline{a_2}~\overline{\cos(\varphi_2-\varphi_1)}\]
Il s’agit d’une valeur moyenne dans le temps.
Comme les sources sont indépendantes, \(\delta\varphi=\varphi_2-\varphi_1\) prend toutes les valeurs possibles, négatives et positives de sorte que \(\overline{\cos(\varphi_2-\varphi_1)}=0\). On a alors : \[\overline{A~A^*}=\overline{a_1^2}+\overline{a_2^2}\]
Par exemple, l’éclairement d’une salle est proportionnel au nombre de lampes allumées.
3.2. Composition de deux vibrations cohérentes
La cohérence peut se traduire par : \[\frac{A_1}{A_2}=\text{cte}\qquad\Rightarrow\qquad\frac{a_1}{a_2}=\text{cte}\quad;\quad\varphi_2-\varphi_1=\text{cte}\]
D’où pour l’énergie : \[\overline{A~A^*}=\overline{a_1^2}+\overline{a_2^2}+2~\overline{a_1}~\overline{a_2}~\overline{\cos(\varphi_2-\varphi_1)}\]
Très souvent un facteur \(\Gamma\) accompagne le double produit. On l’appelle degré de cohérence, mais nous supposerons dans ce qui suit que \(\Gamma=1\) ou \(\Gamma=0\).
4. Composition de vibrations rectangulaires
On se propose de composer deux vibrations \(\{\overrightarrow{OM_1},~\overrightarrow{OM_2}\}\) dirigées suivant deux axes de coordonnées rectangulaires : \[\left\{ \begin{aligned} &x=a~\cos\omega~t\\ &y=b~\cos(\omega~t-\varphi) \end{aligned} \right. \qquad \left\{ \begin{aligned} &\frac{x}{a}=\cos\omega~t\\ &\frac{y}{b}=\cos\omega~t~\cos\varphi+\sin\omega~t~\sin\varphi \end{aligned} \right.\]
 On peut les écrire sous la forme :
On peut les écrire sous la forme :
\[\begin{aligned} &\cos\omega~t~\sin\varphi=\frac{x}{a}~\sin\varphi\\ &\sin\omega~t~\sin\varphi=\frac{y}{b}-\frac{x}{a}~\cos\varphi\end{aligned}\]
Élevant au carré et ajoutant membre à membre : \[\frac{x^2}{a^2}-\frac{2~x~y}{a~b}~\cos\varphi+\frac{y^2}{b^2}=\sin^2\varphi\]
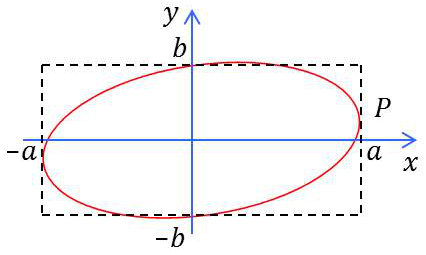
La trajectoire du point \(M\) est une ellipse ; la vibration résultante est dite elliptique. La courbe est inscrite dans un rectangle de côtés (\(2~a,~2~b\)) dont les médianes sont les axes de coordonnées.
Au temps \(t=0\), le point est en \(P(x=a,~y=b~\cos\varphi)\).
Lorsque \(t\) augmente, le sens de variation est donné par : \[\frac{dy}{dt}=b~\omega~\sin\varphi\]
Si l’ellipse est décrite dans le sens trigonométrique, elle est dite gauche. L’ellipse est dite droite dans le cas contraire.
Examinons deux cas particuliers :
\[\begin{aligned} \varphi=(2~k+1)~\frac{\pi}{2}\quad&\Rightarrow\quad\sin\varphi=1\\ \cos\varphi=0\quad&\Rightarrow\quad\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\end{aligned}\]
Équation d’une ellipse d’axes \([Ox,~Oy]\) : \[\varphi=k~\pi\quad\Rightarrow\quad\cos\varphi=\pm1\quad\Rightarrow\quad\Big(\frac{x}{a}+\frac{y}{b}\Big)^2=0\]
L’ellipse est dégénérée en deux droites qui sont les diagonales du rectangle.
4.1. Énergie de vibration
Reprenons les deux composantes : \[\left\{ \begin{aligned} &x=a~\cos\omega~t &&|x|^2=a^2\\ &y=a~\cos(\omega~t-\varphi)\qquad &&|y|^2=b^2 \end{aligned} \right.\]
L’énergie résultante est proportionnelle à \(I=a^2+b^2\) et ne dépend pas du déphasage entre les vibrations.
4.2. Décomposition d’une vibration elliptique
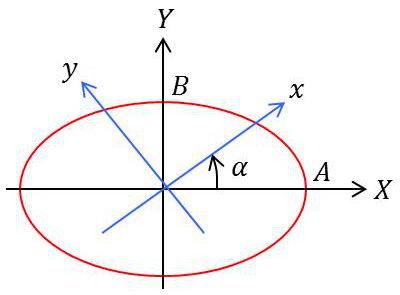 Étant donnée l’ellipse (\(E\)) et la décomposition suivant les axes \(OX\) et \(OY\) :
Étant donnée l’ellipse (\(E\)) et la décomposition suivant les axes \(OX\) et \(OY\) :
Si le déphasage entre les vibrations est \(\varphi=\pm\cfrac{\pi}{2}\), si l’on choisit convenablement l’origine des temps et s’il s’agit d’une ellipse gauche, alors : \[X=A~\cos\omega~t\quad;\quad Y=B~\sin\omega~t\]
Si l’on veut faire la décomposition suivant deux axes quelconques \(Ox,~Oy\), il suffit d’appliquer les formules de changement d’axes (rotation) : \[\left\{ \begin{aligned} &x=X~\cos\alpha+Y~\sin\alpha\\ &y=-X~\sin\alpha+Y~\cos\alpha \end{aligned} \right.\]
5. Composition de deux vibrations circulaires
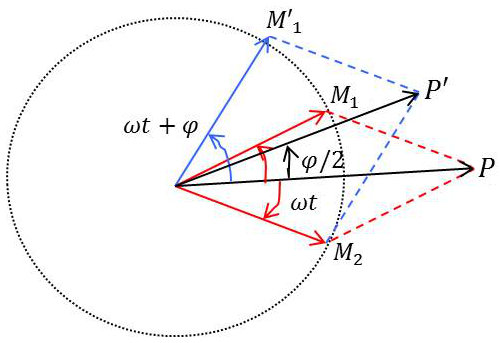 Si les vibrations sont de même sens, il suffit d’adopter la construction de Fresnel classique.
Si les vibrations sont de même sens, il suffit d’adopter la construction de Fresnel classique.
S’il s’agit de vibrations de sens contraire sans déphasage, la construction est facile : par symétrie, le vecteur résultant est porté par l’axe \(Ox\), bissectrice de l’angle \(M_1OM_2\).
Si les vibrations de sens contraire sont de déphasage quelconque, alors le problème est plus complexe.
Le vecteur résultant tourne dans le sens de la vibration qui avance en phase.
Si les amplitudes sont différentes : \[a_1-a_2~<~|\overrightarrow{OP}|~<~a_1+a_2\]
La vibration est elliptique, les demi-axes de l’ellipse étant : \[A=a_1+a_2\quad;\quad B=a_1-a_2\]
Nous allons établir ces résultats analytiquement. On peut choisir les axes \(Ox\) et \(Oy\) de sorte que les vibrations gauche et droite aient pour équations : \[\text{Gauche :}\quad \left\{ \begin{aligned} &x_1=a_1~\cos\omega~t\\ &y_1=a_1~\sin\omega~t \end{aligned} \right. \qquad \text{Droite :}\quad \left\{ \begin{aligned} &x_2=a_2~\cos(\omega~t-\varphi)\\ &y_2=-a_2~\sin(\omega~t-\varphi) \end{aligned} \right.\]
Prenons d’abord deux nouveaux axes \(OX\) et \(OY\) faisant un angle \(\alpha=\frac{\varepsilon}{2}\) avec les premiers. Les équations deviennent alors : \[\left\{ \begin{aligned} &X_1=a_1~\cos(\omega~t-\frac{\varphi}{2})\\ &Y_1=a_1~\sin(\omega~t-\frac{\varphi}{2}) \end{aligned} \right. \qquad \left\{ \begin{aligned} &X_2=a_2~\cos(\omega~t-\frac{\varphi}{2})\\ &Y_2=-a_2~\sin(\omega~t-\frac{\varphi}{2}) \end{aligned} \right.\]
La vibration résultante est : \[\left\{ \begin{aligned} X=X_1+X_2=(a_1+a_2)~\cos(\omega~t-\frac{\varphi}{2})\\ Y=Y_1+Y_2=(a_1-a_2)~\sin(\omega~t-\frac{\varphi}{2}) \end{aligned} \right.\]
La vibration sera :
-
gauche si \(a_1-a_2>0\) ;
-
droite si \(a_1-a_2<0\) ;
-
rectiligne suivant \(Ox\) si \(a_1=a_2\).
On remarquera que la forme de l’ellipse ne dépend pas de \(\varphi\).
Quand \(\varphi\) varie de \(\Delta\varphi\), elle tourne de l’angle dont tournent les axes auxiliaires (\(OX,~OY\)), c’est-à-dire \(\alpha=\cfrac{\Delta\varphi}{2}\).

