1. Généralités

Nous cherchons des solutions de l’équation de propagation qui puissent se mettre sous la forme d’un produit d’une fonction d’espace par une fonction du temps, c’est-à-dire (en choisissant par exemple la variable \(p\) présentant la pression) : \[p(x,~y,~z,~t)=f(x,~y,~z)~g(t)\]

L’équation de propagation : \[\Delta p=\frac{1}{c^2}~\frac{\partial^2p}{\partial t^2}\]

s’écrit alors : \[g~\Delta f=\frac{1}{c^2}~f~g''\qquad\text{soit :}\quad c^2~\frac{\Delta f}{f}=\frac{g''}{g}\]

Le premier membre de cette équation ne dépend que des variables d’espace, le deuxième ne dépendant que du temps. L’égalité n’est possible que si les deux membres sont égaux à une constante que nous choisirons sous une forme négative : \(-\omega^2\).

La fonction \(g(t)\) satisfait à l’équation différentielle : \[g''+\omega^2~g=0\quad\Rightarrow\quad g(t)=\sin(\omega~t+\varphi)\]

Ainsi, le seul fait d’avoir supposé que la loi de variation de la surpression peut être mise sous la forme du produit d’une fonction d’espace par une fonction du temps (et que la vibration persiste sans amortissement au cours du temps) permet d’affirmer que tous les points du fluide vibrent en phase (ou en opposition de phase).

En effet, \(f\) et \(g\) sont ici des fonctions réelles et non des quantités complexes dont il serait ensuite nécessaire de prendre la partie réelle pour obtenir l’expression réelle de \(p\). Il est bien évident que si nous ne faisons pas cette restriction, l’expression de \(p\) peut tout aussi bien représenter une onde progressive.

Dans un tuyau sonore par exemple, la loi de variation : \[p=a~\exp j~\omega~(t-x/c)\]

peut parfaitement se mettre sous la forme du produit d’une fonction d’espace par une fonction du temps soit : \[p=a.\exp(-j~\omega~x/c)~\exp(j~\omega~t)\]

L’expression réelle de la surpression est alors la somme de deux produits du type \(f(x)~g(t)\) : \[p=a~\cos\frac{\omega~x}{c}~\cos\omega~t+a~\sin\frac{\omega~x}{c}~\cos\omega~t\]

et non plus sous la forme d’un produit \(f~g\).

En reportant la constante multiplicative arbitraire \(a\) sur le terme d’amplitude lui-même défini à une constante multiplicative près, nous pourrons prendre \(g(t)=\sin(\omega t+\varphi)\)

Toutes les valeurs de la pulsation \(\omega\) sont bien entendu acceptables à priori, mais l’équation aux amplitudes : \[\Delta f=-\frac{\omega^2}{c}~f\]

doit être satisfaite par la fonction \(f(x,~y,~z)\) représentant la distribution des amplitudes d"oscillations d’un point à l’autre de l’enceinte.

En outre, la présence de l’enceinte limitant le fluide exige que la fonction satisfasse à certaines conditions aux limites. Il en résulte que seules certaines valeurs \(\omega_i\) de \(\omega\) formant en général une suite discrète (ou spectre discontinu) sont en fait acceptables. En conclusion, seules certaines fréquences seront possibles pour le mouvement oscillatoire du fluide enfermé dans l’enceinte.

Le problème de la recherche des vibrations stationnaires du fluide du type \(f(x,~y,~z)~g(t)\) revient donc à rechercher les solutions de l’équation \(\Delta f=\alpha~f\) (avec \(\alpha\) : constante négative) qui satisfasse à certaines conditions aux limites.

Le problème n’a de solutions que pour certaines valeurs de la constante \(\alpha\) qui constituent les valeurs propres de l’opérateur Laplacien (compte tenu des conditions aux limites imposées par l’enceinte). Les valeurs propres étant trouvées, on obtient les pulsations propres correspondantes \(\omega_i\) par la relation : \[\omega_i^2=-c^2~\alpha\]

Pour chacune de ces pulsations, la distribution d’amplitude sera obtenue en résolvant l’équation aux amplitudes \(\Delta f=\alpha_i~f\), compte tenu des conditions aux limites, c’est à dire en cherchant la ou les fonctions propres de l’opérateur Laplacien associé à la valeur propre \(\alpha_i\).

À titre d’exemple et en nous limitant bien entendu au cas des vibrations dans les fluides, nous allons résoudre le problème dans un petit nombre de cas particuliers très simples. Nous obtiendrons pour chaque type d’enceinte une suite de vibrations sinusoïdales possibles (qui ne constituent pas forcément les harmoniques d’un même fondamental).

Le mouvement stationnaire le plus général du fluide dans la cavité serait obtenu par superposition de ces diverses vibrations sinusoïdales avec des phases \(\varphi_i\) arbitraires, la distribution d’amplitude \(f_i(x,~y,~z)\) étant en outre affectée d’un coefficient multiplicatif arbitraire, soit : \[p(x,~y,~z,~t)=\sum_i a_i~f_i(x,~y,~z)~\sin(\omega_i~t+\varphi_i)\]

Nous choisirons comme variable oscillante, de préférence à la surpression \(p\), le potentiel des vitesses \(\Phi(x,~y,~z,~t)\) qui satisfait également à l’équation de propagation :

\[\begin{aligned} \Delta\Phi&=\frac{1}{c^2}~\frac{\partial^2\varphi}{\partial t^2}\\ \Phi(x,~y,~z,~t)&=\psi(x,~y,~z)~\sin(\omega~t+\varphi)\end{aligned}\]

La fonction \(\psi(x,~y,~z)\) qui représente la distribution d’amplitudes du potentiel des vitesses sera souvent désignée pour simplifier le langage sous le nom de potentiel des vitesses. Elle doit, du fait de la présence de l’enceinte ou cavité limitant le fluide, satisfaire à certaines conditions aux limites. Nous nous bornerons à deux cas simples.

En tout point d’une ouverture à l’air libre, la surpression est nulle (en première approximation) et il en est donc de même de \(\cfrac{\partial\Phi}{\partial t}=\cfrac{p}{p_0}\) quel que soit \(t\).

Donc \(\psi(x,~y,~z)\) doit être nul en tout point d’une ouverture à l’air libre, c’est-à-dire sur toute la surface séparant le fluide en vibration de l’atmosphère extérieure ; dans le cas d’un tuyau d’axe vertical empli d’un fluide liquide, cette surface est la surface libre du liquide.

Pour un tuyau sonore ouvert, elle est évidemment beaucoup moins bien définie (nous rejoignons ici les difficultés introduites par les corrections aux extrémités) et nous la confondrons avec la section droite limitant le tuyau ; pour une cavité sphérique percée, nous prendrions la potion de sphère prolongeant l’enceinte et fermant l’ouverture, etc.

Sur toute la surface de l’enceinte supposée parfaitement rigide, la composante normale de la vitesse du fluide est nécessairement nulle ; il en résulte, en désignant par \(\overrightarrow{n}\) le vecteur normal à la surface la relation : \[\overrightarrow{n}\cdot\overrightarrow{\rm grad}(\psi)=0\]

Ceci, sur toute la surface de la cavité limitant le fluide.

2. Problème linéaire. Tuyau sonore

Dans le cas d’un tuyau, il n’y a qu’une seule variable d’espace, donc le Laplacien est : \[\Delta=\frac{\partial^2}{\partial x^2}\]

L’équation aux amplitudes s’écrit : \[\frac{\partial^2\psi}{\partial x^2}=-\frac{\omega^2}{c}~\psi\quad\Rightarrow\quad\psi(x)=a~\cos(\omega~\frac{x}{c}+\alpha)\]

Les conditions aux limites vont fixer les valeurs de \(\omega,\alpha\)

2.1. Tuyau fermé en \(x=0\) et ouvert en \(x=l\)

\(x=0\) : \[|\overrightarrow{\rm grad}(\psi)|=\frac{\partial\psi}{\partial x}=0\quad\Rightarrow\quad\alpha=0~~;~~\psi(x)=a~\cos\frac{\omega~x}{c}\]

\(x=l\) : \[\psi=0\quad\Rightarrow\quad\cos\frac{\omega~l}{c}~~;~~\omega=\frac{c}{l}~\Big(\frac{\pi}{2}+k~\pi\Big)\]

Les longueurs d’onde possibles sont donc données par : \[l=(2~k+1)~\frac{\lambda}{4}\]

On observe un nœud pour \(\psi\) (donc pour \(p\)) à l’ouverture libre et un ventre de pression à l’extrémité fermée.

2.2. Tuyau fermé aux deux bouts

\(x=0,~~x=l\) : \[\frac{\partial\psi}{\partial x}=0\quad\Rightarrow\quad\alpha=0\]

C’est-à-dire : \[\psi(x)=-a\cos\frac{\omega~x}{c}~~\text{et}~~\frac{\omega~l}{c}=k~\pi\quad\Rightarrow\quad l=k~\frac{\lambda}{2}\]

On observe des ventres de pression aux deux extrémités.

2.3. Tuyau ouvert aux deux bouts

\(x=0,~~x=l\) : \[\psi=0\quad\Rightarrow\quad\alpha=\frac{\pi}{2}\]

C’est à dire : \[\psi(x)=-a~\sin\frac{\omega~x}{c}~~\text{et}~~\frac{\omega~l}{c}=k~\pi\quad\Rightarrow\quad l=k~\frac{\lambda}{2}\]

On observe des nœuds de pression aux deux bouts.

3. Problème à symétrie sphérique

Proposons-nous d’étudier les vibrations stationnaires d’un fluide enfermé dans une cavité sphérique de rayon \(R\), en nous limitant aux mouvements dans lesquels la vitesse est radiale (symétrie sphérique). \(\psi\) n’est fonction que de \(R\) et satisfait à l’équation : \[\frac{\partial^2(r~\psi)}{\partial r^2}=\frac{\omega^2}{c^2}~r~\psi\]

Soit : \[\psi(r)=\frac{a}{r}~\sin\Big(\frac{\omega~r}{c}+\alpha\Big)\]

Cherchons les conditions aux limites. Tout d’abord, \(\psi(r)\) doit rester bornée pour \(r=0\) (centre de la cavité), ce qui exige \(\alpha=0\) et par suite : \[\psi(r)=\frac{a}{r}~\sin\frac{\omega~r}{c}\]

En outre, \(|\overrightarrow{\rm grad}(\psi)|=\cfrac{\partial\psi}{\partial r}\) doit s’annuler pour \(r=R\). On a donc : \[-\frac{a}{R^2}~\sin\frac{\omega~R}{c}+\frac{\omega~a}{r~c}~\cos\frac{\omega~R}{c}=0\]

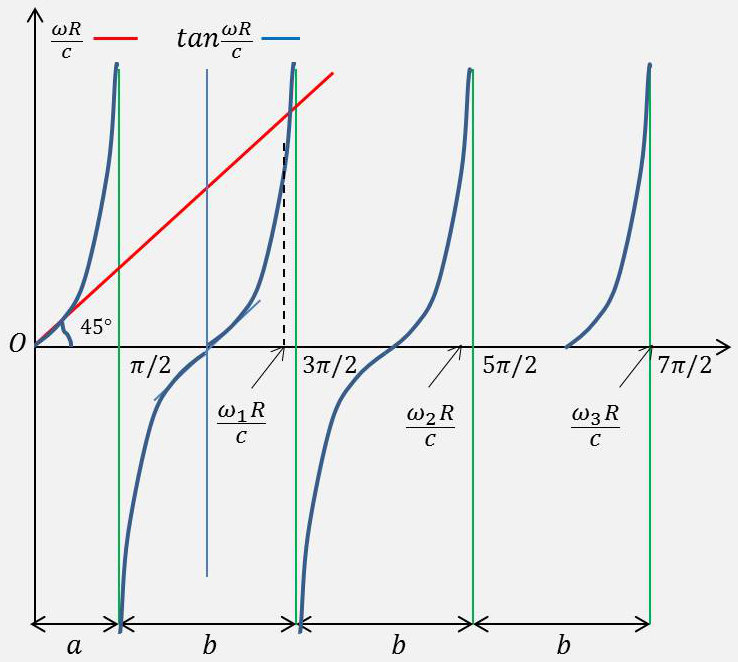
C’est à dire : \[\tan\frac{\omega~R}{c}=\frac{\omega~R}{c}\]

Les solutions sont obtenues au moyen de la construction ci-dessus.

Elles ne forment pas une suite d’harmoniques, mais sont très voisines de la série : \[\omega_k=\Big(k+\frac{3}{2}\Big)~\frac{\pi~c}{r}\qquad\text{surtout pour k élevé.}\]

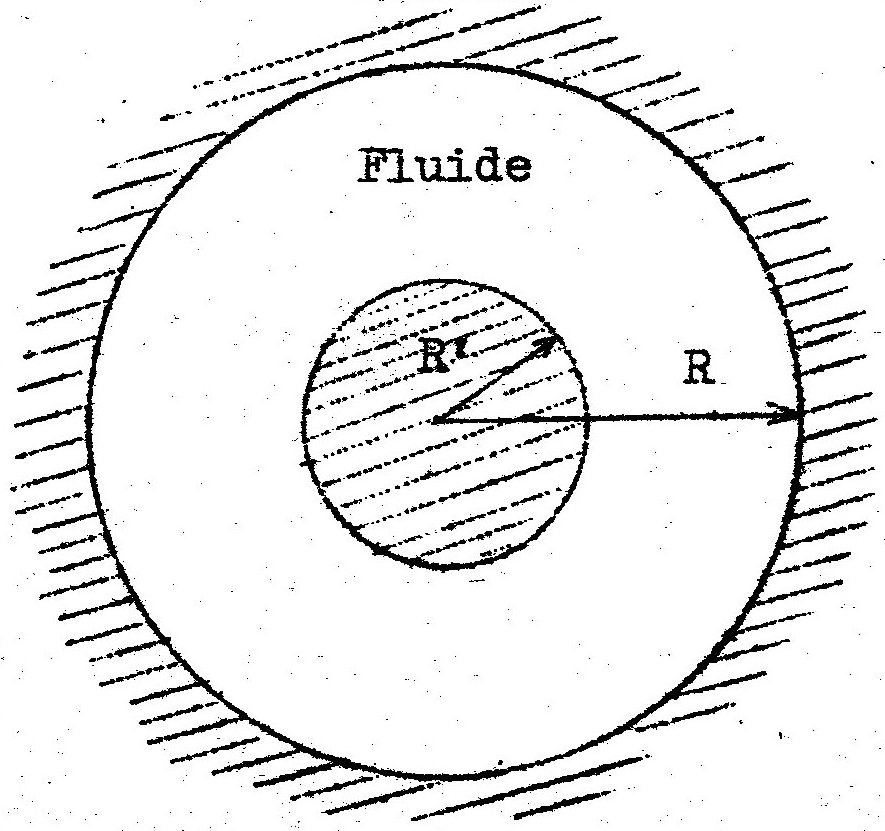Passons maintenant à un fluide enfermé dans l’espace limité par deux sphères concentriques de rayons \(R\) et \(R'\) :

\[\begin{aligned} \psi(r)&=\frac{a}{r}~\sin(\omega~\frac{r}{c}+\alpha)\\ \frac{\partial\psi}{\partial r}&=0\qquad\text{pour :}\quad r=R,~~r=R'\end{aligned}\]

C’est-à-dire :

\[\begin{aligned} &\tan\Big(\frac{\omega~R}{c}+\alpha\Big)=\frac{\omega~R}{c}\\ &\tan\Big(\frac{\omega~R'}{c}+\alpha\Big)=\frac{\omega~R'}{c}\end{aligned}\]

Nous obtiendrons les pulsations propres en éliminant \(\alpha\).

Posons :

\[\begin{aligned} \frac{\omega~R}{c}+\alpha&=\arctan\frac{\omega~R}{c}\\ \frac{\omega~R'}{c}+\alpha&=\arctan\frac{\omega~R'}{c}\end{aligned}\]

Tous calculs faits : \[\tan\frac{\omega(R-R')}{c}=\frac{\omega~c~(R-R')}{c^2+\omega^2~R~R'}\]

On revient naturellement au cas précédent en faisant \(R'=0\).

Remarque

Dans le cas où \(R'=0\) (cavité sphérique), nous avions obtenu une solution en laissant \(\psi(r)\) bornée pour \(r=0\). Vérifions que le déplacement correspondant s’annule pour \(r=0\) bien que contenant un terme en \(1/r^2\). Il suffit de vérifier que : \[\frac{\partial\psi}{\partial r}=0\qquad\text{pour :}~~r=0\]

On peut écrire : \[\frac{\partial\psi}{\partial r}=-\frac{a}{r^2}~\sin\frac{\omega~r}{c}+\frac{\omega~a}{r~c}~\cos\frac{\omega~r}{c}\]

En faisant intervenir les développements limités classiques : \[\frac{\partial\psi}{\partial r}~\cong-\frac{a~\omega^3~r}{3~c^3}\qquad\text{qui s'annule bien pour :}~r=0.\]

4. Vibrations propres pour une enceinte parallélépipédique

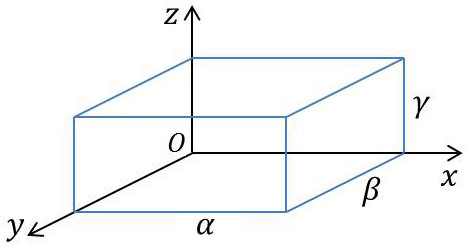L’enceinte de côtés (\(\alpha,\beta,\gamma\))est limitée par les plans : \[x=0,~~x=\alpha,~~y=0,~~y=\beta,~~z=0~~,z=\gamma\]

Cherchons des solutions de l’équation aux amplitudes : \[\Delta\psi=-\frac{\omega^2}{c^2}~\psi\]

qui puissent se mettre sous la forme : \[\psi(x,~y,~z)=f(x)~g(y)~h(z)\]

Le Laplacien s’écrit : \[\Delta\psi=f''~g~h+f~g''~h+f~g~h''\]

L’équation aux amplitudes s’écrira : \[\frac{f''}{f}+\frac{g''}{g}+\frac{h''}{h}=-\frac{\omega^2}{c}\]

Le premier membre est la somme de trois quantités qui ne dépendent chacune que de l’une des trois variables et qui doivent donc être séparément constantes. Nous poserons donc : \[\left\{ \begin{aligned} &\frac{f''}{f}=-\frac{\omega_1^2}{c^2}\quad\Rightarrow\quad f(x)=A_1~\cos\Big(\frac{\omega_1~x}{c}+\psi_1\Big)\\ &\frac{g''}{g}=-\frac{\omega_2^2}{c^2}\quad\Rightarrow\quad f(x)=A_2~\cos\Big(\frac{\omega_2~x}{c}+\psi_2\Big)\\ &\frac{h''}{h}=-\frac{\omega_3^2}{c^2}\quad\Rightarrow\quad f(x)=A_3~\cos\Big(\frac{\omega_3~x}{c}+\psi_3\Big) \end{aligned} \right.\]

La condition \(\overrightarrow{n}\cdot\overrightarrow{grad}(\psi)\) sur les parois s’écrit :

Parois \(x=0\), \(x=\alpha\) : \[\frac{\partial\psi}{\partial x}=0\quad\forall~(y,~z)\qquad\text{donc :}\quad f'_x=0\]

On en déduit immédiatement (avec généralisation):

\[\begin{aligned} &\psi_1=0~~\text{et}~~\frac{\omega_1~\alpha}{c}=l~\pi\quad~~\text{l~: entier}\\ &\psi_2=0~~\text{et}~~\frac{\omega_2~\alpha}{c}=m~\pi\quad\text{m~: entier}\\ &\psi_3=0~~\text{et}~~\frac{\omega_3~\alpha}{c}=n~\pi\quad~~\text{n~: entier}\end{aligned}\]

L’amplitude du potentiel des vitesses a donc pour expression : \[\psi(x,~y,~z)=A~\cos\frac{l~\pi~x}{\alpha}~\cos\frac{m~\pi~y}{\beta}~\cos\frac{n~\pi~z}{\gamma}\quad;\quad A=A_1~A_2~A_3\]

et le potentiel des vitesses devient lui-même : \[\Phi(x,~y,~z,~t)=A~\cos\frac{l~\pi~x}{\alpha}~\cos\frac{m~\pi~y}{\beta}~\cos\frac{n~\pi~z}{\gamma}~\sin(\omega~t+\varphi)\]

\(A\) et \(\varphi\) arbitraires  et  \(\omega=\sqrt{\omega_1^2+\omega_2^2+\omega_3^2}\)

À tout ensemble de trois nombres entiers \((l,~m,~n)\), on peut donc associer un état de vibration du fluide dans l’enceinte, dont la fréquence de vibration est bien déterminée par la relation : \[\nu=\frac{\omega}{2~\pi}=\frac{c}{2}~\sqrt{\frac{l^2}{\alpha^2}+\frac{m^2}{\beta^2}+\frac{n^2}{\gamma^2}}\]

La longueur d’onde de la vibration \((l,~m,~n)\) est par suite donnée par la relation : \[\frac{1}{\lambda}=\sqrt{\frac{l^2}{4~\alpha^2}+\frac{m^2}{4~\beta^2}+\frac{n^2}{4~\gamma^2}}\]

Les nombres d’ondes \(\sigma=1/\lambda\) des divers états vibratoires possibles peuvent être obtenus graphiquement par une construction très simple : le réseau triplement périodique a pour maille élémentaire le parallélépipède de côtés \[\Big\{\frac{1}{2~\alpha},~~\frac{1}{2~\beta},~~\frac{1}{2~\gamma}\Big\}\]

les nœuds du réseau ont pour coordonnées : \[\Big\{\frac{l}{2~\alpha},~~\frac{m}{2~\beta},~~\frac{n}{2~\gamma}\Big\}\]

Il suffit de joindre l’origine à l’un de ces nœuds pour obtenir un segment dont la longueur représente l’un des nombres entiers possibles.

4.1. Recherche d’un nombre d’états vibratoires

On se propose de rechercher le nombre d’états vibratoires de fréquences comprises dans un intervalle donné (\(\nu,~\nu+d\nu\)).

Les nombres d’ondes doivent être compris entre \(\cfrac{\nu}{c}\) et \(\cfrac{\nu+d\nu}{c}\).

On trace les deux sphères ayant ces rayons respectifs et on cherche combien de nœuds du réseau à coordonnées positives sont compris dans l’intervalle situé entre ces deux sphères. L’espace dans lesquels les nœuds doivent se trouver est également situé dans le trièdre formé par les trois demi-axes positifs \(Ox,~Oy,~Oz\).

Dans notre construction graphique, le nombre de nœuds est égal à celui des mailles élémentaires de volume \(\cfrac{1}{8~\alpha~\beta~\gamma}\). Il y a donc par unité de volume \(8~\alpha~\beta~\gamma\) nœuds et le nombre de nœuds compris dans l’espace considéré de volume : \[\frac{1}{8}~4~\pi~(\frac{\nu}{c})^2~d\Big(\frac{\nu}{c}\Big)=\frac{\pi~\nu^2~d\nu}{2~c^3}\]

est donc égal (en désignant par \(V=\alpha~\beta~\gamma\) le volume de l’enceinte) à : \[dn=V~\frac{4~\pi~\nu^2~d\nu}{c^3}\]

C’est là le nombre d’états de vibrations distincts de l’enceinte parallélépipédique de volume \(V\) dont la fréquence est comprise entre (\(\nu,~\nu+d\nu\)).

Le résultat est valable pour une enceinte de forme quelconque. Remarquons toutefois que nous avons conduit le calcul en supposant la maille élémentaire très petite devant l’espace compris entre les deux sphères, donc à fortiori devant le rayon des sphères, ce qui revient à n’étudier que des vibrations de longueur d’onde très petite devant les dimensions \(\alpha,~\beta,~\gamma\) de l’enceinte parallélépipédique.

Dans le cas d’une enceinte de forme quelconque, celle-ci devra être de dimensions très supérieures à la longueur d’onde et en outre ne devra pas présenter de recoins (cavités secondaires) de dimensions comparables à la longueur d’onde.

4.2. Cas des ondes lumineuses

Un calcul tout à fait identique permet de dénombrer les états de rayonnement (rayonnement thermique par exemple) dans le vide, au sein d’une enceinte parallélépipédique.

Le mode de vibrations est simplement deux fois plus élevé, car il s’agit alors de vibrations transversales et chaque vibration peut être décomposée en deux vibrations polarisées à angle droit.

Soit un nombre de vibrations comprises dans l’intervalle (\(\nu,~\nu+d\nu\)) : \[dn=g(\nu)~d\nu=\frac{8~\pi~V~\nu^2~d\nu}{c^3}\]

Passons maintenant à la conception des photons d’énergie \(h~\nu\), qui constituent des corpuscules satisfaisant à la statistique de Bose-Einstein et pour lesquels, par suite, le nombre de corpuscules appartenant à un niveau d’énergie \(U_i\) de dégénérescence \(g_i\) est donné par la relation (le multiplicateur de Lagrange \(\alpha\) disparaît du fait que le nombre de photons dans l’enceinte n’est pas tenu à rester invariable lors de la mise à l’état d’équilibre thermique) : \[\frac{N_i+g_i}{N_i}=\exp\frac{U_i}{kT}\quad\Rightarrow\quad N_i=\frac{g_i}{\exp(U_i/k~T)-1}\]

Nous considérons ici le domaine des énergies \([h~\nu,~h~(\nu+d\nu)]\) contenant \(g(\nu)~d\nu\) cellules. L’énergie totale des photons contenus dans ce domaine représente l’énergie totale contenue dans l’enceinte sous forme de rayonnements de fréquences appartenant à l’intervalle \([\nu,~\nu+d\nu]\).

On trouve ainsi, par unité de volume de l’enceinte, une densité d’énergie vibratoire correspondant à cette bande de fréquences :

\[\begin{aligned} U(\nu)~d\nu&=\frac{h~\nu}{V}~\frac{g(\nu)~d\nu}{\exp(U_i/k~T)-1}\\ U(\nu)~d\nu&=\frac{8~\pi~h~\nu^3}{c^3}~\frac{d\nu}{\exp(U_i/k~T)-1}\end{aligned}\]

On a coutume, en général, de rapporter la densité d’énergie à un bande de longueurs d’onde d’étendue (\(\lambda,~\lambda+d\lambda\)) ; la densité d’énergie rayonnante est dès lors \(u_{\lambda}~d\lambda\) avec : \[|u_{\lambda}d\lambda|=|U(\nu)d\nu|\quad\text{et}\quad \nu=\frac{c}{\lambda}\quad\text{soit}\quad |d\nu|=|\frac{c}{\lambda^2}d\lambda|\]

On a dès lors, pour la densité d’énergie correspondant aux rayonnements (ondes stationnaires) de longueurs d’onde de l’intervalle (\(\lambda,\lambda+d\lambda\)), l’expression \(u_{\lambda}d\lambda\) avec : \[u_{\lambda}=\frac{8~\pi~h~c~\lambda^{-5}}{\exp(h~\nu/k~T)-1}\qquad\text{Formule de Planck}\]

5. Résonateur de Helmoltz

Dans l’étude des vibrations propres d’un fluide enfermé dans une cavité sphérique, nous sommes loin d’avoir épuisé tous les modes de vibrations possibles. Nous nous sommes en effet restreints à l’étude des mouvements du fluide qui présentent la symétrie sphérique (mouvements radiaux).

Il est bien évident que d’autres modes sont possibles ; leur étude revient à rechercher toutes les fonctions propres de l’opérateur Laplacien dont l’expression générale en coordonnées sphériques \(r,~\theta,~\varphi\) (rayon vecteur, colatitude et longitude) est nettement plus compliquée dès que l’on abandonne la symétrie sphérique où la seule variable est \(r\).

Un résonateur de Helmoltz est constitué par une cavité creuse de forme sphérique (mais ce n’est pas indispensable) qui présente deux ouvertures à l’air libre : une ouverture principale ou goulot \(O\) et, à l’extrémité diamétralement opposée, une ouverture secondaire \(O'\) destinée à être appliquée sur l’oreille de l’observateur.

Nous pourrons considérer que l’ouverture secondaire est bouchée par le tympan de l’observateur et que tout se passe par suite, en ce qui concerne les vibrations de l’air contenu dans le résonateur, comme si elle n’existait pas.

Supposons que l’observateur, portant le résonateur à l’oreille, soit placé devant une source sonore de faible intensité dont la fréquence, initialement très basse, est progressivement élevée.

L’expérience montre que, lorsque la fréquence atteint une certaine valeur \(\nu_0\), le son perçu par l’observateur est considérablement renforcé par l’interposition du générateur. L’air contenu dans le résonateur entre en résonance et les variations de pression acoustique à l’intérieur du résonateur (directement perçues par l’oreille placée en \(O'\)) sont beaucoup plus importantes que les variations de pression produites au niveau du résonateur par la source sonore.

La théorie de ce phénomène est considérablement simplifiée par le fait que la fréquence de résonance \(\nu_0\) est relativement basse et que la longueur d’onde qui correspond à cette fréquence est de façon générale très supérieure aux dimensions du résonateur ; il en résulte que la pression de l’air à l’intérieur du résonateur joue alors le rôle d’un ressort repoussant la tranche d’air qui se trouve à l’aplomb du goulot \(O\).

Cette tranche d’air a un diamètre égal à celui du goulot \(O\) et on peut en gros estimer que son épaisseur est de l’ordre de grandeur du rayon du goulot ; la surface du goulot se comporte en effet, au point de vue de l’émission d’ondes sonores dans l’atmosphère extérieure, comme une sphère pulsante de rayon très petit devant la longueur d’onde.

Nous reportant à l’expression donnant la loi de variation de la vitesse radiale en fonction de \(r\) au voisinage de la sphère pulsante, nous observons que cette vitesse radiale n’est de l’ordre de la vitesse radiale au contact de la sphère (amplitude \(a~\omega\)) que tant que la valeur de \(r\) est du même ordre que celui de la sphère pulsante, soit par exemple \(\varepsilon<r<2~\varepsilon\).

Bien que les circonstances ne soient pas exactement les mêmes, nous pouvons admettre que la tranche d’air oscillant à l’aplomb du goulot se comporte comme un piston coulissant sans frottement dans un cylindre de section \(S\) (section du goulot).

La masse du piston étant égale à celle d’une tranche d’air de volume sensiblement égal à \(S.r\), on a : \[m=K~\rho_0~S^{3/2}\]

\(K\) : coefficient de proportionnalité de l’ordre de grandeur de l’unité.

Étudions d’abord les oscillations libres du piston constitué par cette tranche d’air ; nous obtiendrons ainsi les vibrations propres du résonateur en l’absence d’excitation extérieure.

Soit \(P_0\) la pression extérieure (constante) ; le piston qui représente la tranche d’air en mouvement est soumis sur sa droite à la pression \(P_0\), sur sa gauche à une pression \(P_0+\delta p\), \(\delta p\) étant uniquement fonction de l’écart \(x\) du piston par rapport à sa position de repos ; on a effet (\(V\) désignant le volume de l’enceinte et le coefficient de dilatation du gaz qu’elle contient) : \[\delta p=-\frac{\theta}{\chi}=-\frac{x~S}{V}~\frac{1}{\chi}=-\frac{S}{\chi~V}~x\]

Le piston est donc soumis à une force (comptée positivement suivant les \(x\) croissants) : \[f=p~S=-\frac{S^2}{\chi~V}~x\]

Il prend dès lors une accélération telle que : \[m~\frac{d^2x}{dt^2}=-\frac{S^2}{\chi~V}~x\qquad\text{ou encore :}\quad \frac{d^2x}{dt^2}+\frac{S^{1/2}}{\chi~\rho_0~K~V}~x=0\]

Le mouvement du piston est un mouvement pendulaire de pulsation : \[\omega_0=\sqrt{\frac{S^{1/2}}{\chi~\rho_0~K~V}}\]

de fréquence : \[\nu_0=\frac{1}{2~\pi}\frac{c~S^{1/4}}{\sqrt{K~V}}\qquad\text{Pour rappel :}~c^2=\frac{1}{\chi~\rho_0}\]

La constante \(K\) est de l’ordre de l’unité ; pour une enceinte de volume \(V=1~\rm dm^3=10^{-3}~m^3\) et une surface de goulot \(S=1~\rm cm^2\), nous trouvons une fréquence de résonance \(\nu_0=150~\rm Hz\), c’est-à-dire \(\lambda_0=2~\rm m\).

Cette longueur d’onde est donc très supérieure aux dimensions du résonateur et ceci justifie à postériori l’approximation que nous avons faite en supposant uniforme la pression de l’air à l’intérieur du résonateur.

5.1. Amortissement des vibrations propres

Bien entendu, le mouvement harmonique que nous avons obtenu ne saurait se maintenir indéfiniment ; plusieurs causes d’amortissement interviennent en effet et nous les avons jusqu’ici négligées.

Tout d’abord, les dilatations et compressions de l’air dans le résonateur entraînent des échanges de chaleur avec les parois de l’enceinte ; ces échanges irréversibles entraînent un accroissement d’entropie et par suite une transformation progressive en chaleur de l’énergie de vibration. En outre, le mouvement de la tranche gazeuse est freiné par des phénomènes de viscosité. Enfin, le résonateur émet dans l’air extérieur des ondes acoustiques qui emportent progressivement son énergie de vibration.

Toutes ces causes d’amortissement peuvent en gros être considérées comme équivalente à une force de frottement visqueux, du type : \[F'=-f~\frac{dx}{dt}\]

agissant sur le mouvement de la tranche gazeuse.

Posant alors : \(\alpha=\cfrac{f}{2~m~\omega_0}\quad\)(coefficient d’amortissement) et remarquant que \(\alpha\ll 1\), nous obtenons pour le mouvement de la tranche d’air, et par suite pour la loi de variation de la surpression dans le résonateur, une loi sinusoïdale amortie du type : \[\delta p=\delta p_0~\exp(-\alpha~\omega_0~t)~\sin(\omega~t+\varphi)\]

avec :  \(\omega=\omega_0~\sqrt{1-\alpha^2}~\cong~\omega_0\)   dont le décrément logarithmique est \(\delta=2~\pi~\alpha\).

5.2. Vibrations forcées

Lorsqu’il est soumis à une force extérieure exercée par une onde acoustique dont la surpression agit sur la tranche d’air située en \(O\), le résonateur entre en vibration forcées et tous les calculs que nous avons faits pour le pendule amorti par frottement visqueux se transposent intégralement.

En particulier, le rapport entre les amplitudes des variations de pression à l’intérieur et à l’extérieur du résonateur est grand à la résonance où il atteint une valeur égale à la surtension \(1/2~\alpha\) ; il reste supérieur à \(1/\alpha~\sqrt{2}\) dans toute la bande de fréquences (bande passante) comprise entre les limites \((1\pm\alpha)~\nu_0\).

Supposons par exemple que l’amortissement du résonateur abandonné à lui-même soit tel que l’amplitude des oscillations de pression soient divisées par \(e\) après 5 oscillations, soit un décrément logarithmique \(\delta=1/5\), ce qui correspond à un amortissement \(\alpha=\delta/2~\pi~\cong~1/30\). La surtension a alors pour valeur 15.

Il en résulte que l’amplitude des variations de pression à l’intérieur du résonateur est à la résonance 15 fois plus importante que celle des variations de pression dans l’onde sonore excitatrice.

L’intensité du son perçu par l’oreille de l’observateur est 225 fois plus grande que celle qu’il percevrait directement, sans interposition du résonateur. Le résonateur renforce donc considérablement les sons dont la fréquence coïncide avec la fréquence propre \(\nu_0\) (dans un intervalle de fréquence d’étendue approximative \(2~\alpha~\nu_0\)).

Remarque : en présence d’un son complexe (fondamental et harmoniques), le résonateur renforce sélectivement celui des harmoniques (s’il existe) dont la fréquence se situe dans sa bande passante.

5.3. Estimation de l’amortissement

Nous avons assimilé la tranche gazeuse en mouvement (dans le cas des oscillations libres) à un piston soumis d’un côté à la pression oscillante qui règne à l’intérieur du résonateur, de l’autre à une pression constante \(P_0\) ; cela revient à ne pas tenir compte des fluctuations de pression extérieure dues à l’onde divergente qui est émise par le goulot.

En fait, ces fluctuations de pression, bien que décroissant en raison inverse de la distance, ne sont nullement négligeables à une distance \(r\) du goulot. Nous ne devons cependant pas en tenir compte, car la masse gazeuse en mouvement est d’épaisseur très supérieure à \(r\) et n’est donc soumise sur sa droite qu’à une surpression négligeable.

D’autre part, la vitesse des couches gazeuses diminue rapidement quand on s’éloigne du goulot et il en résulte que l’inertie opposée à la surpression intérieure par l’ensemble de cette masse gazeuse (importante, mais dont la vitesse moyenne est très inférieure à celle de la tranche située à l’aplomb du goulot) est du même ordre que l’inertie qu’opposerait à cette surpression une masse gazeuse d’épaisseur \(r\) dont tous les éléments oscilleraient à la vitesse maximum.

On peut éviter ces considérations et retrouver les résultats que nous avons obtenus sans faire appel au mouvement de la tranche gazeuse : il suffit de considérer que l’ouverture à l’air libre se comporte comme une source d’ondes sonores analogues à une sphère pulsante de rayon \(r\) (celui du goulot) très petit devant la longueur d’onde des vibrations émises.

Pour une amplitude d’oscillation \(a\) des couches d’air à l’aplomb du goulot, la surpression à l’intérieur de ces couches (donc à l’extérieur du résonateur) est (voir chapitre précédent) : \[\delta p=-\rho_0~a~r~\omega^2~\sin\omega~(t-r/c)\]

Pour la vitesse radiale : \[v_r=a~\omega~\cos\omega~(t-r/c)\]

Pour l’accélération : \[\gamma_r=-\alpha~\omega^2~\sin\omega~(t-r/c)\]

On a donc la relation : \[\delta p=\rho_0~r~\gamma_r\]

Soit, sur toute la surface du goulot, une force due à la surpression intérieure : \[S~\delta p=\rho_0~S~r~\gamma_r\]

Ceci indique que le mouvement de ces couches gazeuses est le même que si la surpression s’exerçait sur un piston de surface \(S\) et de masse \(m=\rho_0~S~r\), ainsi que nous l’avions émis plus haut.

On peut d’une manière analogue obtenir un ordre de grandeur de l’amortissement dû à une onde acoustique émise par le goulot (cet amortissement est inévitable alors que la part de l’amortissement due aux phénomènes de viscosité et aux échanges thermiques avec la paroi du résonateur pourrait théoriquement être supprimée si le résonateur était constitué par une enceinte adiabatique et l’air qu’il contient par un gaz parfait).

Nous pouvons dans une approximation grossière assimiler la surface \(S\) du goulot à une portion de surface \(S\) d’une sphère pulsante de rayon \(r\) égal à celui du goulot, soit une puissance moyenne émise dans l’atmosphère sous forme d’une onde acoustique divergente : \[\overline{P}=\frac{S}{4~\pi~r^2}~2~\pi~\rho_0~a^2~\frac{\omega^4~r^4}{c}=S~\rho_0~a^2~\frac{\omega^4~r^4}{2~c}\]

qui emporte à chaque oscillation une énergie \(\cfrac{2~\pi}{\omega}~\overline{P}\) prise à l’énergie de vibration du gaz enfermé dans le résonateur.

Cette énergie d’oscillation varie donc à chaque période de : \[\delta E=-\frac{2~\pi}{\omega}~\overline{P}~\cong-\frac{\pi~S}{c}~\rho_0~a^2~\omega^3~r^3\]

L’énergie d’oscillation \(E\) du résonateur est égale à l’énergie potentielle de compression maximum du gaz qu’il contient, soit : \[E~\cong~V~\frac{\theta_m^2}{2~\chi}=V~\frac{a^2~S^2}{2~\chi~V^2}=\frac{a^2~S^2}{2~\chi~V}\]

On observe à chaque période une variation d’énergie \(\delta E\) soit une variation d’amplitude \(\delta E/2~E\).

Le décrément logarithmique \(\delta\) du mouvement oscillatoire amorti du résonateur est dès lors : \[\delta=-\frac{\delta E}{2~E}=\frac{\chi~V}{a^2~S^2}\rho_0~\frac{\pi~S~a^2~\omega^3~r^2}{c}\]

Avec  \(\chi~\rho_0=1/c^2\)  et  \(\pi~r^2=S\), il vient : \[\delta~\cong~V~\frac{\omega^3}{c^2}=8~\pi^3~\frac{V}{\lambda^3}\]

Soit, au voisinage de la résonance : \[\lambda~\cong~\frac{2~\pi~\sqrt{V}}{S^{1/4}}\quad;\quad\delta~\cong~\frac{S^{3/4}}{\sqrt{V}}\]

Application numérique : \[V=10^{-3}~{\rm m^3}~;~S=10^{-4}~\rm m^2\quad\Rightarrow\quad\delta\cong\frac{1}{30}~;~\alpha\cong\frac{1}{200}\]

Le renforcement d’intensité apporté par le résonateur serait dans ces conditions (à la résonance) égal à 10 000.