1. Vitesse de propagation des interactions

Pour le physicien, le monde physique a une existence indépendante de lui et extérieure à lui. Le principe de relativité en est l’expression formelle : les lois générales peuvent être exprimées sous une forme valable pour tous les observateurs. Mais pour être étudiées, les lois de la nature nécessitent deux systèmes de référence :

• les systèmes de coordonnées, repérant les positions ;

• les horloges, fixées dans chaque système de référence, indiquant le temps.

Le principe de relativité exige l’invariance des équations exprimant les lois générales dans tout changement de coordonnées et de temps, pour passer d’un système de référence à l’autre. Il existe des systèmes de référence dans lesquels un corps se meut librement, c’est-à-dire sur lequel aucune force n’agit : ce corps poursuit son mouvement à vitesse constante. Ces systèmes sont dits référentiels d’inertie. Tous les référentiels en translation uniforme par rapport à un tel système sont eux-mêmes des référentiels d’inertie.

La mécanique classique suppose une propagation instantanée des interactions car ces interactions à l’instant \(t\) sont décrites au moyen d’un potentiel ne dépendant que des positions des particules à ce même instant. Or, l’expérience montre que les interactions instantanées n’existent pas dans la nature. Un changement d’un des corps en interaction ne commence à influencer les autres qu’après une certaine durée. On peut donc définir une vitesse finie de propagation de l’interaction, c’est-à-dire sa vitesse maximum. Cela implique que tous les mouvements réels des corps de la nature se font à une vitesse inférieure à cette vitesse maximum. Il résulte, en particulier du principe de relativité, que cette vitesse d’interaction doit être la même pour tous les systèmes d’inertie. Cette vitesse est donc une constante universelle.

Le principe de relativité de Galilée reposait sur des vitesses infinies de propagation des interactions. Il a été contredit par le principe de relativité d’Einstein (1905), combinaison du principe de relativité et de la valeur finie de la vitesse maximum de propagation des interactions. L’expérience de Michelson (1881) contenait en germe le principe de relativité d’Einstein et a contraint à une révision des lois de la mécanique classique. En même temps, elle ne montrait aucune dépendance de la vitesse de la lumière par rapport au mouvement de l’observateur, c’est à dire que la vitesse de la lumière dans le vide apparaissait comme étant la vitesse maximum d’interaction. Deux postulats sont implicitement contenus dans la théorie de la relativité :

1) La loi d’invariance du sens d’écoulement du temps
Le seul concept irréversible est celui d’entropie. Mais il semble raisonnable de supposer que la seconde loi de la thermodynamique permet de préciser le sens du temps de tous les référentiels. On prendra comme sens positif du temps celui qui va dans le sens du désordre statistique croissant, ou de la dégradation de l’énergie en chaleur.

2) La loi de reproductibilité des propriétés fondamentales
Pour un observateur au repos par rapport à l’étalon, les propriétés (par exemple longueur d’onde d’une raie spectrale donnée, période d’un matériau radioactif, etc.) sont parfaitement définies et reproductibles. On les appelle longueurs propres, temps propres, etc.

2. Concept de simultanéité

La mécanique classique, basée sur le principe de Galilée, utilise un temps absolu, indépendant du système de référence. Il en résulte une loi de composition des vitesses (addition vectorielle), en complet désaccord avec le principe d’Einstein, puisqu’elle conduit à des vitesses de propagation des interactions différentes dans chaque système d’inertie.

Considérons deux événements localisés (par exemple l’émission d’un point lumineux) dans un système de référence \(S\) aux points \(P_1\) et \(P_2\). Nous dirons que ces événements sont simultanés si les deux signaux lumineux atteignent au même instant le milieu géométrique du segment \(P_1 P_2\).

Pour un observateur en mouvement par rapport à \(S\) les deux signaux ne seront évidemment plus perçus en même temps. L’observateur en mouvement ayant quitté le milieu \(M\) au moment de l’émission rencontrera le front de l’onde issue d’une des extrémités avant l’autre. Donc si nous changeons de référentiel, la notion de simultanéité disparaît. En conséquence, l’intervalle de temps qui sépare deux événements ayant lieu dans des points séparés dans l’espace dépend du système de référence de l’observateur.

Dans la transformation de Galilée : \[\big\{(x',~y',~z')=f(x,~y,~z)~;~t=t' \big\}\]

Dans une transformation plus générale : \[\big\{(x',~y',~z',~t')=g(x,~y,~z,~t)\big\}\]

Cette transformation doit rester linéaire de façon à maintenir l’équivalence entre tous les points de l’espace-temps.

Deux physiciens sont situés à bord d’un vaisseau spatial en \( A_1 \) et \( B_1 \). Les réacteurs sont coupés et le vaisseau est situé loin de toute planète et de tout astre. Ils imaginent donc que leur habitacle est au repos dans l’univers.

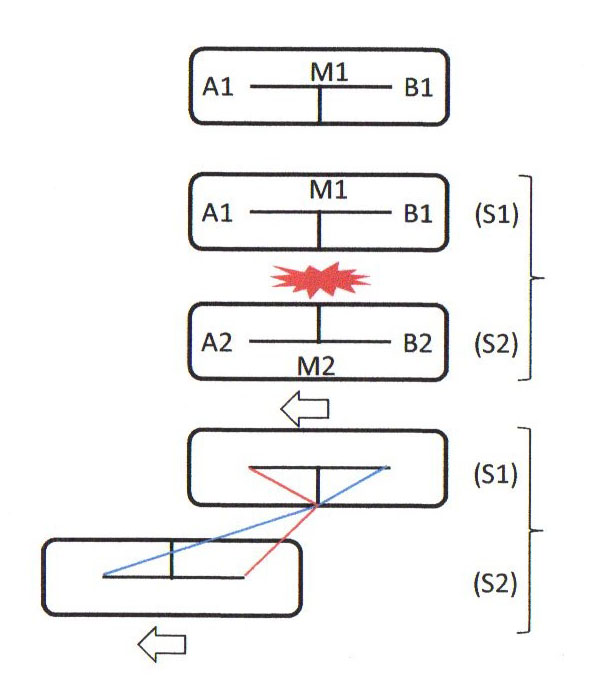À l’intérieur de leur vaisseau (quelques centaines de mètres de longueur), ils peuvent synchroniser leurs chronomètres à partir de l’observation d’une étincelle émise à mi-distance (au point \( M_1 \)). La lumière, voyageant à la vitesse \(c\) met le même temps pour atteindre les deux points \( A_1 \) et \( B_1 \).

Par hasard, un second vaisseau de même longueur, habité lui aussi par deux physiciens et animé d’une vitesse \(v\) par rapport au premier, croise le vaisseau \(S_1\). Au moment exact du croisement, une étincelle instantanée jaillit. Elle peut être observée par les quatre physiciens qui déclenchent leurs chronomètres.

La lumière, partie de \(M_1\) atteint \(A_1\) et \(B_1\) au même moment. Pour les physiciens de \(S_1\), les arrivées du signal en \(A_1\) et \(B_1\) sont donc des événements simultanés. Par contre, la lumière partie de \(M_2\) à la vitesse finie \(c\) arrivera en \(B_2\) avant d’arriver en \(B_1\), tandis qu’elle arrivera en \(A_2\) après être arrivée en \(A_1\). Ainsi, les arrivées de la lumière en \(A_2\) et en \(B_2\) ne sont pas des événements simultanés.

Les physiciens de \(S_2\) tiendront le même raisonnement, les rôles étant simplement inversés : des événements simultanés pour l’une des équipes ne le sont pas pour l’autre. Aucun des groupes ne peut mettre en évidence son état de repos ou de mouvement. Les deux systèmes galiléens sont rigoureusement équivalents et aucune expérience de physique ne permet de trancher la question. Leur tort est de vouloir exporter leur temps. Les physiciens de \(S_1\) définissent un temps valable dans le référentiel \(S_1\). Ceux de \(S_2\) définissent un autre temps valable dans le référentiel \(S_2\).

L’impossibilité de mettre en évidence l’état de repos absolu ou de mouvement rectiligne uniforme absolu ainsi que le principe de la constance de la vitesse de la lumière par rapport à tout repère galiléen entraînent le rejet de la notion de temps absolu. Le désaccord ne sera toutefois sensible que si la vitesse \(v\) des vaisseaux est de l’ordre de grandeur de \(c\).

Ainsi, les notions de temps absolu et de simultanéité absolue s’évanouissent. Deux événements qui ont lieu dans deux endroits différents peuvent être simultanés par rapport à un système galiléen \(S_1\) et être séparés par un intervalle de temps fini par rapport à un autre système galiléen \(S_2\). Cette proposition est surprenante et pourtant celle-ci ne nous étonne pas : deux événements qui ont lieu à des temps différents en un même point sont séparés par un intervalle d’espace fini par rapport à un autre système.

Par exemple, par rapport à l’avion dans lequel nous voyageons, nous déjeunons et nous dînons au même endroit. Pourtant, par rapport au sol, le déjeuner et le dîner à la même heure sont séparés par des milliers de kilomètres. Et pourtant nous n’avons fait qu’intervertir les mots espace et temps dans les propositions énoncées ci-dessus. Pourquoi cette impossibilité de définir un temps absolu ? Tout simplement parce qu’il n’existe pas de courrier de vitesse infinie.