1. Généralités

Nous avons jusqu’à présent défini provisoirement le gaz parfait comme un gaz vérifiant la loi de Mariotte à toute température :

• \(p~v=m~r~T\) : pour une masse de m grammes

• \(p~v~=~n~R~T\) : pour n moles de gaz

Pour cela nous avons introduit un fait d’expérience supplémentaire en remarquant que les échelles des thermomètres à gaz tendent vers une limite commune quand la pression du gaz utilisé tend vers zéro.

À présent, nous allons pouvoir donner du gaz parfait une définition complète en nous intéressant à son énergie interne.

2. Expérience de Joule - Gay-Lussac

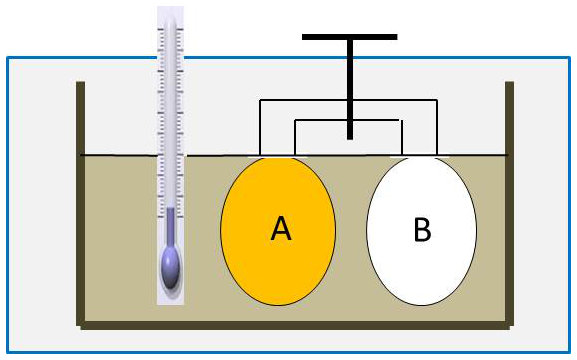Un récipient formé de deux parties \(A\) et \(B\) que l’on peut mettre en communication par un robinet est plongé dans un calorimètre rempli d’eau (rappelons que le calorimètre est entouré d’une enceinte adiabatique interdisant tout échange de chaleur avec le milieu extérieur).

Au début de l’expérience, \(A\) est rempli du gaz à étudier, \(B\) est vide, le robinet est fermé. On note la température de l’eau du calorimètre. On ouvre le robinet, le gaz se répand dans \(B\) et les pressions s’équilibrent en \(A\) et \(B\). On observe que la température de l’eau du calorimètre n’a pas changé.

Nous en déduisons que :

• le travail reçu par le gaz est nul (le récipient qui le contient étant indéformable) ;

• l’énergie interne de l’eau n’a pas changé, le travail qu’elle a reçu étant nul (volume invariable), la chaleur qu’elle a cédée est nulle ;

• par suite, le gaz qui ne peut recevoir de chaleur que de l’eau du calorimètre (enceinte adiabatique) n’a reçu aucune chaleur de cette transformation où sa température n’a pas changé (équilibre thermique avec l’eau) et où seul son volume a varié.

En définitive, l’énergie interne du gaz est la même dans l’état initial (volume \(V_A\) et température \(T\)) et dans l’état final (volume \(V_{A+B}\) et température \(T\)).

L’énergie interne d’un gaz ne varie donc pas de façon appréciable dans une transformation à température constante ; en d’autres termes, elle ne dépend que de la température du gaz.

Cette expérience est peu précise, la masse du gaz et par suite sa capacité calorifique étant très faibles devant la masse et la capacité calorifique de l’eau et des accessoires, mais elle permet de donner une définition précise du gaz parfait.

Nous désignerons sous le nom de gaz parfait un gaz idéal qui suivrait à toute température la loi de Boyle-Mariotte et celle de Joule.

Pour une masse donnée de gaz parfait, nous pouvons écrire : \[p~v~=~\varphi(T)\quad;\quad \frac{\partial U}{\partial v}~=~0\]

La différence d’énergie interne entre deux états voisins infiniment proches : \[dU~=~C_v~dT+(l-p)~dv\]

On en tire : \[\frac{\partial U}{\partial T}~=~C_v\quad;\quad \frac{\partial U}{\partial v}~=~l-p\]

La première équation donne la dérivée partielle \(\partial U/\partial T\) égale à la capacité calorifique à volume constant de la masse de gaz considérée, soit n moles.

La seconde équation nous apprend que si le gaz est un gaz parfait satisfaisant à la loi de Joule : \[\frac{\partial U}{\partial v}~=~l-p~=~0\quad\Rightarrow\quad l~=~p\]

La différentielle \(dU\) se réduit donc à \(C_v~dT\). C’est une différentielle totale. Par suite, le coefficient \(C_v\) de \(dT\) ne dépend que de T.

On a donc : \[\frac{\partial C_v}{\partial v}=0\quad;\quad dU~=~C_v(T).dT\]

Par contre, nous ne savons rien sur la variation de \(C_v\) avec \(T\), mais nous verrons qu’une étude microscopique des gaz permet de la prévoir.

3. Relation de Mayer

Nous avons vu que pour une masse de gaz parfait égale à n moles : \[l~=~(C_p-C_v)~\frac{p}{n~R}\quad\Rightarrow\quad C_p-C_v~=~n~R\]

C’est la relation de Mayer, liant les capacités calorifiques à pression et à volume constant d’une masse d’un gaz parfait égale à n moles.

On a coutume de désigner sous le nom de capacité calorifique moléculaire la capacité calorifique d’une masse égale à 1 mole. Nous observons alors que la différence des capacités calorifiques moléculaires à \(p\) et \(v\) constants d’un gaz parfait est égale à \(R\), constante des gaz parfaits.

Quant à la différence des chaleurs spécifiques (capacités calorifiques d’une masse égale à 1 gramme), elle est égale à : \[c_p-c_v~=~\frac{R}{M}~=~r\qquad~M~\text{masse moléculaire}\]

Remarque

Il faut bien noter qu’ici les chaleurs sont exprimées en unités mécaniques (joules) et, par suite, les capacités calorifiques en joules par kelvin.

Si nous voulons exprimer les capacités calorifiques en calories par kelvin, les formules deviennent :

\[\begin{aligned} &C_p-C_v~=~n~\frac{R}{J}\approx 2~n\\ &M~(c_p-c_v)=\frac{r}{J}\approx 2\end{aligned}\]

4. Compression (ou détente) adiabatique ou réversible d’un gaz parfait

Nous avons obtenu, pour n moles d’un gaz parfait : \[\lambda=C_v~\frac{v}{n~R}\quad;\quad\mu=C_p~\frac{p}{n~R}\]

Une transformation infinitésimale, adiabatique et réversible est donc régie par : \[C_v~\frac{v}{n~R}~dp+C_p~\frac{p}{n~R}~dv=0\]

Soit, en posant  \(\gamma=\cfrac{C_p}{C_v}\) : \[v~dp+\gamma~p~dv=0\qquad\text{ou}\qquad\frac{dp}{p}+\gamma~\frac{dv}{v}=0\]

Considérons maintenant une transformation adiabatique finie et admettons que l’on puisse considérer \(\gamma\) comme constant dans le domaine de températures décrit par le gaz.

L’équation différentielle s’intègre alors sous la forme simple : \[p~v^{\gamma}~=~\text{cte}\]

C’est la formule de Laplace, valable pour une transformation adiabatique réversible.

Notons qu’elle ne s’applique en toute rigueur qu’aux gaz parfaits, et encore faut-il que l’on puisse considérer que \(\gamma\) reste constant pendant la transformation.

4.1. Variation de température dans une détente adiabatique

Pour une transformation infinitésimale, réversible et adiabatique d’un gaz parfait :

\[\begin{aligned} &\frac{dT}{T}~=~\frac{dp}{p}+\frac{dv}{v}\\ &\frac{dp}{p}+\gamma\frac{dv}{v}=0\end{aligned}\]

On en tire :

\[\begin{aligned} \frac{dT}{T}&=(1-\gamma)~\frac{dv}{v}\\ \text{ou encore :}\qquad\qquad\\ \gamma~\frac{dT}{T}&=(\gamma-1)~\frac{dp}{p}\end{aligned}\]

Pour une détente finie, et si \(\gamma\) peut être considéré comme constant, on peut intégrer ces relations sous la forme simple : \[T~v^{\gamma-1}=\text{cte}\qquad\text{ou encore}\qquad T~p^{(1-\gamma)/\gamma}=\text{cte}\] On rappelle en outre que : \[p~v^{\gamma}~=~cte\]

Ces relations permettent de calculer par exemple l’abaissement de température qui accompagne une détente adiabatique réversible d’un gaz parfait.

Prenons par exemple le cas d’une masse d’air, considéré comme gaz parfait (\(\gamma\approx 7/5\)), passant de façon adiabatique et réversible d’un état initial (\(T_0=273~K~;~p_0=10~atm\)) à un état final où sa pression est de 1 atmosphère.

Tous calculs faits, on trouve : \[\frac{T}{T_0}=0,53\quad;\quad T\approx~144~K\quad;\quad t=-129~^oC\]

L’abaissement de température est donc considérable.

4.2. Calcul du travail

Cherchons à calculer le travail reçu par le gaz dans une transformation adiabatique et réversible le faisant passer de l’état \([p_0,~v_0]\) à l’état \([p_1,~v_1]\).

Tout au long de la transformation : \[p~v^{\gamma}~=~p_0~v_0^{\gamma}~=~p_1~v_1^{\gamma}\]

En faisant le remplacement  \(p~\rightarrow~(p_0~v_0^{\gamma})/v^{\gamma}\), nous obtenons : \[W=-p_0~v_0^{\gamma}\int_{v0}^{v1}\frac{dv}{v^{\gamma}}=\frac{p_0~v_0^{\gamma}}{1-\gamma}~\{v_0^{1-\gamma}-v_1^{1-\gamma}\}\]

Soit en définitive : \[W~=~\frac{p_1~v_1-p_0~v_0}{\gamma-1}\]

Ou encore, si le nombre de moles est n : \[W~=~\frac{n~R}{\gamma-1}~(T_1-T_0)\]

Le travail reçu est évidemment positif s’il s’agit d’une compression produisant un échauffement (rappelons que l’on a toujours \(\gamma\geq 0\)).

Remarque

Nous aurions pu obtenir ce résultat directement en écrivant \(W=\Delta U\), égalité valable pour une transformation adiabatique quelconque.

Or, on a : \[\Delta U~=~C_v~\Delta T~=~n~R~\frac{C_v}{C_p-C_v}~\Delta T\]

On retrouve le résultat précédent.

Cette égalité reste valable pour une transformation adiabatique irréversible. La formule de Laplace n’est toutefois plus valable et les variations de température qui accompagnent une variation donnée de volume (ou de pression) ne sont plus les mêmes.