1. Le théorème du viriel en mécanique

Pour un physicien curieux d’étymologie, le terme viriel évoque de par la rime celui de potentiel, mot rencontré dans nos premières leçons de physique qui étonnait déjà les lycéens que nous étions : un potentiel ne se voyait pas. La sensation est quelque peu analogue avec le viriel du jeune étudiant en thermodynamique.

Un demi-siècle plus tard, et en l’écrivant, je m’intéresse pour une fois à ce mot initié par Rudolf Clausius en 1870. Un mot qui viendrait, selon toute vraisemblance, du latin vis dont le pluriel est vires c’est-à-dire forces, mot auquel le savant aurait complété par le suffixe iel, un peu aussi comme dans courriel.

Comme eût dit l’inspecteur Bourrel (alias Raymond Souplex), personnage principal du feuilleton TV des années 1970 intitulé les Cinq dernières minutes : « Bon Dieu, mais c’est bien sûr ! potentiel vient du latin potens qui signifie puissant ».

En substance, le théorème du viriel est énonce que l’énergie cinétique est égale et de signe contraire à la moitié de l’énergie potentielle mécanique.

Énoncé d’origine

Considérons un ensemble stable de particules de masses m, repérées par leurs positons \(\overrightarrow{r}\), leurs vitesses \(\overrightarrow{v}\) sur lesquelles s’exercent des forces \(\overrightarrow{f}\).

Selon ce théorème et abstraction faite des indices croisés (pour alléger la formule) : \[\sum\frac{1}{2}m~\overline{v^2}=-\frac{1}{2}\sum\overline{(\overrightarrow{r}\cdot\overrightarrow{f})}\]

On en retient souvent la forme : \[2~E_c+E_p=0\]

2. De la mécanique à la thermodynamique

2.1. De l’aspect mécanique

Quand on considère un gaz dans son aspect microscopique (assemblée de molécules), on perçoit une certaine analogie avec un système isolé de N corps de masses constantes ne subissant que les seules forces gravitationnelles de ses voisines.

Les actions sont les suivantes :

– Force gravitationnelle exercée sur le corps \((i)\) par les autres corps \((j\neq i)\) : \[f_i=-\sum_{j\neq i}G~m_i~m_j~\frac{1}{|r_i-r_j|^2}\qquad\text{c'est-à-dire :}\quad f=G~\frac{m~m'}{d^2}\]

– Application du principe fondamental de la dynamique : \[f_i=m_i~\Big(\frac{d^2r_i}{dt^2}\Big)\qquad\text{c'est-à-dire :}\quad f=m~\overrightarrow{\gamma}\]

En intégrant par rapport au temps et en introduisant la masse inerte, on aboutit à relation aux énergies potentielle, cinétique et inertielle : \[-\frac{1}{2}~\sum_{j\neq i}G~\frac{m_i~m_j}{|r_i-r_j|}+m_i~\Big(\frac{dr_i}{dt}\Big)^2 =\frac{1}{2}~\frac{d^2}{dt^2}~\Big(\sum_i m_i~r_i^2\Big)\]

Le troisième terme, masse inerte correspondant au moment d’inertie, disparaît car, le système étant isolé, cette inertie est une constante.

Il reste alors : \[-\frac{1}{2}~\sum_{j\neq i}G~\frac{m_i~m_j}{|r_i-r_j|}+m_i~\Big(\frac{dr_i}{dt}\Big)^2=0\]

D’où le résultat attendu : \[E_p+2~E_c=0\qquad\text{ou}\qquad E_c=-\frac{1}{2}~E_p\]

2.2. Vers l’aspect thermodynamique

L’équation d’état d’un gaz réel peut être obtenue, tout au moins de manière approximative, à partir du théorème dit du viriel en mécanique, appliqué par Clausius à la théorie des gaz. Il cherchait à relier les notions de température et de chaleur aux mouvements des molécules de gaz.

Soient \((x,~y,~z)\) les coordonnées du centre de gravité et \((u,~v,~w)\) les composantes de vitesse d’une molécule de masse \(m\).

Soient \((X,~Y,~Z)\) les composantes de la force qui lui est appliquée à l’instant \(t\).

Il désignait par \(V\) le viriel des forces agissant sur le gaz : \[V=\frac{1}{2}~\sum(X~x+Y~y+Z~z)\]

3. Viriel de Clausius

Décomposons le viriel en deux termes :

• \(V_e\): viriel extérieur correspondant aux forces extérieures (action des parois, gravitation, etc.) ;

• \(V_i\) : viriel intérieur correspondant aux forces intermoléculaires.

3.1. Calcul du viriel intérieur

Pour calculer le viriel intérieur, on supposera que les forces intermoléculaires sont des forces centrales ne dépendant que de la distance.

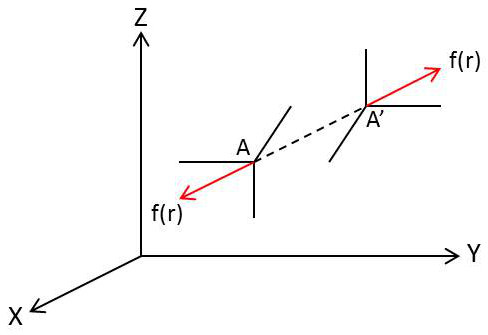
Nous désignerons par \(f(r)\) la force de répulsion qu’exercent l’une sur l’autre deux molécules dont les centres sont à la distance \(r\) (cette force de répulsion est négative pour deux molécules qui ne sont pas en contact).

Le viriel intérieur comprend \(N~(N-1)\) termes qui correspondent à l’action sur chaque molécule des \((N-1)\) autres molécules.

Considérons un couple de deux molécules \(A\) et\(A'\) dont la distance des centres est \(r\).

Il conduit à deux termes dans le viriel.

– Action de la molécule \((x',~y',~z')\) sur la molécule \((x,~y,~z)\) \[X=\frac{x-x'}{r}~f(r)\qquad~\text{etc.}\]

soit un terme de viriel : \[\frac{1}{2}~\Big\{\frac{x~(x-x')}{r}~;~\frac{y~(y-y')}{r}~;~\frac{z~(z-z')}{r}\Big\}~f(r)\]

– Action de la molécule \((x,~y,~z)\) sur la molécule \((x',~y',~z')\) \[X=\frac{x'-x}{r}~f(r)\qquad~\text{etc.}\]

soit un terme de viriel : \[\frac{1}{2}~\Big\{\frac{x'~(x'-x)}{r}~;~\frac{y'~(y'-y)}{r}~;~\frac{z'~(z'-z)}{r}\Big\}~f(r)\]

En remarquant que : \[r^2=(x'-x)^2+(y'-y)^2+(z'-z)^2\]

le viriel s’écrit : \[V_i=\frac{1}{2}~\sum r~f(r)\]

\(\sum\) est étendue à tous les \(\cfrac{N~(N-1)}{2}\) couples de molécules.

3.2. Calcul du viriel extérieur

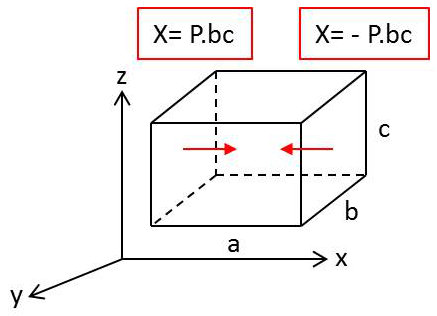On ne considère que l’action des parois du récipient que nous supposerons pour simplifier parallélépipédique et de côtés \((a,~b,~c)\) suivant \((X,~Y,~Z)\).

Les forces suivant \(Ox\) exercées par les parois sur le gaz sont les forces équilibrant la pression du gaz sur les faces de l’enceinte perpendiculaires à \(Ox\) et distantes de \(a\). En désignat par \(P\) la pression, ces deux forces sont opposées et de grandeur \(P~bc\).

Leur contribution au viriel extérieur est donc, en désignant par \(x\) et \(x-a\) les abscisses de ces deux faces et \(V\) le volume du gaz : \[\frac{1}{2}\{-P~bc~x+P~bc~(x-a)\}=-\frac{1}{2}~P~abc=-\frac{1}{2}~P~V\]

On aura également deux termes identiques avec les deux autres parois, soit au total un viriel extérieur : \[V_e=-\frac{3}{2}~P~V\]

Le théorème du viriel s’écrit alors : \[\sum \frac{1}{2}~m~c^2=\frac{3}{2}~P~V-\frac{1}{2}~\sum r~f(r)\]

Pour une mole de gaz, l’équipartition de l’énergie conduit à : \[\sum\frac{1}{2}~m~c^2=\frac{3}{2}~R~T\]

On a donc pour une mole de gaz : \[P~V=R~T+\frac{1}{3}~\sum r~f(r)\]

Ce qui montre bien l’écart que les forces intermoléculaires introduisent par rapport à l’équation des gaz parfaits.

4. Calcul approximatif de \(\sum r~f(r)\)

Nous considèrerons les molécules comme des sphères rigides élastiques de diamètre \(\sigma\).

Lorsqu’une molécule vient au contact d’une autre, les deux centres se rapprochent à une distance inférieure ou égale à \(\sigma\) et une force de répulsion très importante intervient qui crée le rebondissement.

Lorsque la distance des centres est supérieure à \(\sigma\), les deux molécules s’attirent. La loi de force est donc : \[\left\{ \begin{aligned} &f(r)=0\qquad\qquad\qquad\qquad~r=\infty\\ &f(r)<0\qquad\qquad\qquad\qquad~\sigma<r<\infty\\ &f(r)>0~~~(\text{très grand})\qquad~r<\sigma \end{aligned} \right.\]

Considérons tous les couples de deux molécules formés avec une molécule A et les (N – 1) autres. Ces molécules exercent sur la molécule A des forces d’attraction si elles ne la touchent pas et des forces de répulsion si elles la touchent.

Nous supposerons que la concentration moléculaire est uniforme dans l’enceinte et égale à \(N/V\) à l’extérieur de la sphère de protection de la molécule considérée.

Le nombre de centres moléculaires situés à une distance du centre de la molécule comprise entre \(r\) et \(r+dr\) est alors : \[\frac{N}{V}~4\pi~r^2~dr\]

Soit un nombre total de couples de molécules dont la distance est comprise entre \(r\) et \(r+dr\), \(N/2\) fois plus élevé (et non pas \(N\) car, en recommençant le calcul pour les \(N\) molécules, on obtient deux fois chaque couple).

Le nombre \(dn\) de tels couples est donc : \[dn=\frac{2\pi~N^2}{V}~r^2~dr\quad;\quad~r>\sigma\]

On a donc une contribution à la somme \(\sum\cfrac{1}{3}~\{r~f(r)\}\) des couples de molécules non au contact : \[\frac{2\pi~N^2}{3~V}\int_{\sigma}^{\infty} f(r)~r^3~dr-\frac{a}{V}\]

avec \(a > 0\) puisque \(f(r) < 0\) pour tous ces couples.

Calculons maintenant la contribution des couples de molécules au contact, pour lesquels \(r < \sigma\) mais très légèrement.

Isolons dans ce but une molécule A. Elle exerce sur toute molécule qui tente d’approcher son centre à distance inférieure à \(\sigma\) une force de répulsion très grande qui interdit au centre de toute molécule de se trouver à une distance inférieure à \((\sigma-\varepsilon)\) du centre de A, avec \(\varepsilon\ll\sigma\).

Cela peut s’exprimer en considérant que toute molécule dont le centre se trouve à une distance \(r\) telle que \(\sigma<r<\sigma-\varepsilon\) du centre de A possède, de ce fait, une énergie potentielle due à la répulsion de A et dont la valeur est égale au travail exercé par cette force de répulsion lorsque le centre de la molécule qui heurte A est repoussé de la distance \(r\) à la distance \(\sigma\), soit une énergie potentielle : \[E(r)=\int_r^{\sigma} f(r)~dr\quad;\quad~r<\sigma\]

\(f(r)=-\dfrac{E(r)}{dr}\) étant la force de répulsion très grande qui apparaît lors du choc.

La concentration en centres moléculaires à l’intérieur de la sphère de protection de A est donc de la forme (distribution de Boltzmann) : \[c(r)=\frac{N}{V}~\exp\Big\{-\frac{E(r)}{k~T}\Big\}\]

puisqu’elle est égale à \(N/V\) pour \(r = \sigma\) à la limite de la sphère de protection.

Le nombre des centres moléculaires distants du centre de A d’une quantité comprise entre \(r\) et \(r + dr\) avec \(r<\sigma\) est donc : \[\frac{N}{V}~4\pi~r^2\exp\Big\{-\frac{E(r)}{k~T}\Big\}~dr\]

avec les conditions :

\[\begin{aligned} &E(r)=0 &&r=\sigma\\ &E(r)=\infty &&r\leq\sigma\end{aligned}\]

car il ne peut y avoir de centres à distance inférieures à \(\sigma-\varepsilon\).

Le nombre de couples de molécules distantes de \(r\) à \(dr\) près \((r<\sigma)\) est donc : \[\frac{N^2}{V}~2\pi~r^2~\exp\Big\{-\frac{E(r)}{k~T}\Big\}~dr\]

Par suite, la contribution des couples au contact à la somme \(\sum r~f(r)/3\) est : \[\int_{\sigma-\varepsilon}^{\sigma} f(r)~\frac{N^2}{3~V}~2\pi~r^3~\exp\Big\{-\frac{E(r)}{k~T}\Big\}~dr\approx \frac{N^2}{3~V}~2\pi~\sigma^3\int_{\sigma-\varepsilon}^{\sigma} f(r)~\exp\Big\{-\frac{E(r)}{k~T}\Big\}~dr\]

Mais \(f(r)=-dE(r)/dr\) et l’intégrale a donc pour valeur : \[k~T\exp\Big\{-\frac{E(r)}{k~T}]_{\sigma-\varepsilon}^{\sigma}=kT\]

car on sait que : \[E(\sigma)=0\quad;\quad~E(\sigma-\varepsilon)=\infty\]

La contribution des couples au contact est donc : \[\frac{2}{3}~N~\pi~\sigma^3~N~k~T=\frac{b}{V}R~T\]

En ayant introduit le covolume \[b=\frac{2}{3}~N~\pi~\sigma^3\]

L’équation d’état s’écrit donc en définitive : \[P~V=R~T-\frac{a}{V}+R~T~\frac{b}{V}\]

soit : \[\Big(P+\frac{a}{V^2}\Big)~V=R~T~\Big(1+\frac{b}{V}\Big)\]

\(b\) étant en général très petit devant \(V\), on pourra écrire : \[1+\frac{b}{V}\cong\Big(1-\frac{b}{V}\Big)^{-1}\]

Et on retrouve de la sorte l’équation de Van der Waals : \[\Big(P+\frac{a}{V^2}\Big)(V-b)=R~T\]

En fait, nous avons fait une approximation assez grossière en considérant la concentration moléculaire comme égale à \(N/V\) en tout point à l’extérieur de la sphère de protection.

En réalité, l’attraction de la molécule augmente un peu la concentration en son voisinage (formule de Boltzmann) et la concentration moléculaire, pour \(r>\sigma\), comprend donc un terme en \(\exp\{-E(r)/kT\}\) qui doit être pris en considération dans le calcul de la constante \(a\).

Nous retiendrons simplement que cette constante doit en conséquence dépendre de la température \(T\) du gaz.