1. Introduction

Nous avons déjà observé que les transformations naturelles des systèmes physiques tendent à les rapprocher de l’état d’équilibre. Elles ont par suite une direction bien déterminée, ce qui entraîne leur caractère d’irréversibilité.

Il nous faut alors reconnaître que la thermodynamique classique, telle que nous l’avons jusqu’à présent développée, ne saurait en fait s’appliquer à l’étude de tels processus irréversibles. Nous avons en effet restreint notre étude à celle des systèmes thermodynamiques, c’est-à-dire des systèmes physiques dont l’état peut être complètement défini par un ensemble de coordonnées macroscopiques dites variables thermodynamiques.

De telles coordonnées d’ensemble ne sont en toute rigueur définies que pour des états d’équilibre thermodynamique (d’où leur caractère essentiellement statique) ou tout au moins pour des états infiniment voisins d’un état d’équilibre (d’où la conséquence que seules les transformations quasi statiques se prêteront bien à l’analyse).

Nous allons esquisser maintenant les grandes lignes d’une étude systématique des processus réels, qui conserve le caractère macroscopique de la thermodynamique. Cette étude systématique constitue la thermodynamique des phénomènes irréversibles dont les bases ont été jetées dès 1931 par Onsager.

2. Forces et flux

Considérons par exemple la loi de Fourier qui régit l’écoulement de chaleur entre deux régions de températures différentes d’un même corps. Supposons qu’une plaque indéfinie, à faces planes et parallèles, d’un matériau homogène, ait ses deux faces maintenues à des températures différentes \(T\) et \(T + \Delta T\).

L’expérience montre qu’un écoulement continu de chaleur a lieu au travers de la plaque. Si l’épaisseur de la plaque est \(e\), la quantité de chaleur \(Q\) qui traverse par unité de temps une portion de plaque de surface S est : \[Q=K~\frac{S}{e}~\Delta T\]

\(K\) est un coefficient de proportionnalité qui dépend du matériau considéré et de sa température et que l’on désigne sous le nom de conductibilité calorifique du matériau (supposé homogène et isotrope).

Dans le cas général où deux régions d’un corps quelconque sont maintenues à des températures différentes \(T_1\) et \(T_2\), on observe, après un temps plus ou moins long, l’établissement d’un régime permanent de distribution de températures et d’écoulement de chaleur.

La température en chaque point \(M\) du matériau reste invariable au cours du temps, c’est-à-dire : \(T = T(m)\).

La quantité de chaleur qui traverse par unité de temps un élément de surface \(dS\) entourant le point \(M\) est représentée par le flux à travers cet élément \(dS\) d’un vecteur \(i_Q\), le vecteur courant de chaleur qui est défini à partir de la distribution de température \(T\) par la relation : \[\overrightarrow{i}_Q=-K~\overrightarrow{grad}(T)\]

\(K\) est la conductibilité calorifique locale qui en toute rigueur dépend de \(T\).

Cette relation est à rapprocher de celle qui exprime le flux de courant électrique à travers un matériau de conductibilité électrique \(\sigma\), soit, en régime permanent : \[\overrightarrow{i}=-\sigma~\overrightarrow{grad}(V)\]

Le flux de chaleur entraîné par un déséquilibre permanent de température présente donc de grandes analogies avec le flux de charges électriques qu’entraîne un déséquilibre de potentiel.

Bien d’autres phénomènes irréversibles présentent cette propriété de pouvoir être traduits par une loi expérimentale dite loi phénoménologique qui exprime la proportionnalité d’un flux à gradient.

Citons par exemple les phénomènes de diffusion d’un constituant chimique dans un mélange non homogène : le flux de ce constituant (quantité traversant normalement l’unité de surface dans l’unité de temps) est proportionnel au gradient de concentration de ce constituant dans le mélange.

Tous ces phénomènes présentent le même caractère général : un déséquilibre entraîne un écoulement qui tend à réduire le déséquilibre qui lui donne naissance et dont l’importance est proportionnelle à la grandeur du déséquilibre, du moins tant que le déséquilibre n’est pas trop important.

L’expérience montre aussi que des phénomènes nouveaux et d’un grand intérêt apparaissent lorsque deux causes distinctes de déséquilibre interviennent simultanément. Il se produit alors une interaction entre les écoulements irréversibles qui résultent de ces déséquilibres, de telle sorte que le même écoulement peut être occasionné par des déséquilibres et par suite des forces de natures différentes.

Par exemple, un écoulement de matière au sens d’un mélange gazeux peut être entraîné par un gradient de concentration. C’est le phénomène ordinaire de la diffusion, mais l’écoulement de matière peut aussi apparaître, dans un milieu homogène, sous l’action d’un gradient de température : c’est le phénomène de la diffusion thermique.

Un autre exemple est fourni par les phénomènes thermoélectriques que nous étudierons un peu plus loin. Le passage du courant électrique dans une chaîne de conducteurs \(A-B-A\) tend à établir une différence de température entre les jonctions \(A-B\) et \(B-A\) : c’est l’effet Peltier.

Inversement, le maintient à températures différentes des deux jonctions fait apparaître dans la chaîne une force électromotrice : c’est l’effet thermoélectrique.

3. Relations d’Onsager

Nous venons de voir qu’un certain nombre de causes (en l’occurrence des déséquilibres) peuvent entraîner conjointement un certain nombre d’effets communs (en l’occurrence des écoulements ou flux irréversibles).

Nous désignerons ces causes sous le nom de forces et les représenterons par des quantités \(X_i\). Nous désignerons les conséquences sous le nom de flux et les représenterons par des quantités \(J_i\).

Nous réserverons le même indice aux forces et aux flux qui sont normalement associés en l’absence de toute autre cause de déséquilibre. Par exemple, le même indice sera affecté à l’écoulement de chaleur et à la force qui le fait apparaître de la façon la plus évidente, en l’occurrence la force associée à un gradient de température.

De même, nous affecterons le même indice au flux de courant et à la force qui résulte d’un déséquilibre électrique, au flux de matière et à la force qui résulte d’un gradient de concentration etc.

Toutefois, dans le cas général, l’un quelconque des flux peut être entraîné par l’une quelconque des forces. Nous écrirons donc l’ensemble de relations le plus général liant les flux aux forces, sous une forme linéaire valable tant que les déséquilibres ne sont pas trop importants : \[J_i=\sum_j L_{ij}~X_j\]

Relations qui expriment qu’un flux irréversible déterminé est causé, non pas seulement par le type de déséquilibre qui lui est couramment associé, mais par le concours éventuel de toutes sortes de déséquilibres de natures diverses.

Les coefficients \(L_{ij}~(i,~j=1,~n)\) sont désignés sous le nom de coefficients phénoménologiques.

Ceux qui sont du type \(L_{ii}\) correspondent aux effets simples. On trouve parmi eux la conductibilité calorifique, la conductibilité électrique, le coefficient de diffusion ordinaire, etc.

Les coefficients \(L_{ij}~(i\neq j)\) correspondent aux effets croisés qui résultent de l’interaction entre divers phénomènes irréversibles (par exemple coefficient de diffusion thermique).

3.1. Théorème d’Onsager

Le théorème fondamental établi par Onsager à partir de considérations générales sur la réversibilité à l’échelle microscopique peut s’établir ainsi :

Si l’ensemble des flux \(J_i\) et des forces associées \(X_i\) est choisi de façon convenable, la matrice des coefficients phénoménologiques est symétrique, soit : \[L_{ij}=L_{ji}\qquad\forall i,~j\]

3.2. Choix des forces et des flux

Il sera toujours possible de considérer les phénomènes irréversibles comme intervenant dans un système thermiquement isolé ; on introduira au besoin dans le système les sources éventuelles de chaleur.

L’état du système, en équilibre ou non, pourra être décrit par un ensemble de paramètres \(A_1,~A_2,~\dots,~A_n\) (par exemple températures locales, pressions locales, etc.).

Soient \(A_i^0\) les valeurs de ces paramètres qui correspondent à l’équilibre thermodynamique ; on pourra aussi bien définir l’état du système par les différences : \[a_i=A_i-A_i^0\]

qui représentent les écarts à l’équilibre.

L’entropie \(S\) du système est maximum à l’équilibre, c’est-à-dire pour \(a_i=0\). Pour un ensemble de \(a_i\) quelconques, l’entropie est plus faible, soit un accroissement (négatif) d’entropie d’équilibre que nous pourrons mettre, tant que les \(a_i\) ne sont pas trop grands, sous la forme : \[\Delta S=-\frac{1}{2}~\sum_{ik} s_{ik}~a_i~a_k\quad;\quad s_{ki}=s_{ik}\]

Les \(s_{ik}\) sont des constantes et la forme quadratique \(\sum_{ik} s_{ik}~a_i~a_k\) est toujours positive.

Suivant Onsager, il conviendra pour étudier les phénomènes irréversibles qui se produisent dans un tel système lorsqu’on l’écarte de l’équilibre, de choisir comme flux les dérivées par rapport au temps des variables \(a_i^0\), soit : \[J_i=\frac{da_i}{dt}=a_i^0\]

Et d’introduire comme forces associées les quantités : \[X_i=\frac{\partial(\Delta S)}{\partial a_i}=-\sum_k s_{ik}~a_k\]

Nous remarquons alors que la vitesse d’accroissement de l’entropie du système, soit : \[\frac{d(\Delta S)}{dt}=\Delta^0S\]

s’exprime sous la forme simple : \[\Delta^0S=\sum_i \frac{a_i^0~\partial(\Delta S)}{\partial a_i}=-\sum_{ik} s_{ik}~a_i~a_k=\sum_i J_i~X_i\]

Cette relation est d’une extrême importance, car il nous sera alors possible dans de nombreux cas de calculer, par de simples considérations microscopiques, le taux d’accroissement de l’entropie au cours du temps dans le phénomène irréversible et de la mettre sous la forme de produits de flux et de forces associées dont nous obtenons directement les expressions sans avoir à faire intervenir explicitement les variables d’état \(a_i\).

Remarque

Divers choix peuvent être faits pour les variables d’état \(A_i\). Il en résulte que le taux d’accroissement de l’entropie \(\Delta^0S\) peut s’exprimer de diverses façons, c’est-à-dire peut être réparti de diverses manières en une somme de produits de flux et de forces associées du type \(J_i~X_j\).

Quelle que soit la répartition choisie, nous pourrons toujours écrire des relations phénoménologiques du type : \[J_i=\sum_j L_{ij}~X_j\]

et les coefficients seront liés par l’ensemble des relations d’Onsager : \[L_{ij}=L_{ji}\]

Tout se ramène donc à calculer la vitesse d’accroissement de l’entropie au cours du temps, dans un système hors d’équilibre. Or, nous savons que bien qu’en toute rigueur l’entropie ne soit définie que pour un système en équilibre, il est généralement possible, lorsque le déséquilibre n’est pas trop important \(^{(1)}\) de considérer le système comme formé d’un certain nombre de parties séparément en équilibre interne bien qu’elles ne soient pas en équilibre entre elles, et de calculer l’entropie du système comme somme des entropies des diverses parties.

\(^{(1)}\) Le déséquilibre sera jugé comme pas très important lorsque les coordonnées thermodynamiques locales peuvent être considérées comme uniformes dans les parties du système assez importantes pour contenir beaucoup de molécules. Ceci est indispensable pour que les principes de la thermodynamique s’appliquent à chaque partie individuellement.)

Ce procédé qui consiste en fin de compte à figer momentanément l’évolution naturelle d’un système en équilibre sera très utile dans l’étude des réactions chimiques.

4. Démonstration des relations d’Onsager

4.1. Fondements

La démonstration des relations d’Onsager que nous ne ferons qu’esquisser repose sur trois fondements :

1. La théorie des fluctuations (étude des écarts spontanés à l’équilibre d’un système thermiquement isolé abandonné à lui-même depuis un temps très long).

2. La réversibilité microscopique, c’est-à-dire la réversibilité des phénomènes d’interaction individuelle à l’échelle atomique. Ces phénomènes suivent les lois de la mécanique (mécanique classique ou mécanique quantique) et les mouvements qui en résultent sont parfaitement réversibles comme nous l’avons déjà constaté dans l’étude microscopique de l’expérience de Joule : une complexion dans laquelle les positions des molécules seraient les mêmes et leur vitesse changée de signe est tout aussi probable que la complexion observée.

   Il en résulte que, si l’on observe une suite de fluctuations en remontant dans le temps (par exemple, en déroulant un fil à l’envers), la séquence obtenue est réglée par les mêmes lois que la séquence effectivement décrite par le système, et constitue une séquence normale de fluctuations.

3. L’hypothèse introduite plus ou moins explicitement par Onsager, suivant laquelle les lois qui lient les dérivées par rapport au temps des paramètres d’écart \(a_j\) à ces écarts eux-mêmes sont encore valables dans le domaine des écarts infinitésimaux introduits par les fluctuations spontanées du système autour de l’équilibre.

Signalons en passant que la réversibilité microscopique n’est plus applicable dans le cas où une force magnétique (changement de signe avec la vitesse) agit sur des particules chargées. Les relations d’Onsager en présence d’une induction \(B\) doivent alors s’écrire : \[L_{ij}(B)=J_{ji}(-B)\]

ce qui implique que les coefficients du type \(L_{ij}\) sont des fonctions paires de l’induction \(B\).

4.2. Démonstration

Nous considérons un système thermiquement isolé que nous avons abandonné assez longtemps à lui-même pour qu’il ait atteint (au point de vue macroscopique) l’équilibre thermodynamique.

Nous savons qu’en fait de faibles fluctuations subsistent indéfiniment autour de l’état d’équilibre qui correspond à l’entropie maximum. Nous représentons les fluctuations par un ensemble d’écarts : \[a_i=A_i-A_i^0\qquad\text{fonctions du temps}\]

Soit \(P(a_1,~\dots,~a_n)~da_1~\dots~da_n\) la probabilité pour qu’une observation instantanée indique des écarts \(a_i\) compris entre \([a_i,a_i+da_i]\), etc.

Nous savons que \(P\) est proportionnel au nombre de complexions \(W\) qui caractérise l’état du système décrit par l’ensemble des écarts \(a_i\), c’est-à-dire à la quantité \(\exp(\Delta S/K)\) en vertu de la relation de Boltzmann : \[P(a_1,~\dots,~a_n)~da_1~\dots~da_n=\frac{\exp(\Delta S/K)~da_1~\dots~da_n}{\int...\int \exp(\Delta S/K)~da_1~\dots~da_n}\]

L’intégrale étant étendue à tout le domaine de variation des \(a_i\).

Introduisons les quantités : \[X_i=\frac{\partial(\Delta S)}{\partial a_i}=-\sum_k s_{ik}~a_k\]

et cherchons à calculer la valeur moyenne au cours du temps (ou parmi un ensemble de systèmes identiques à un instant donné) de la quantité \(a_i~X_j\) :

Il vient alors : \[\overline{a_i~X_j}=\int...\int P(a_1,~\dots,~a_n)~da_1~\dots~da_n\]

Soit en remarquant que : \[X_i=\frac{\partial(\Delta S)}{\partial a_i}=k~\frac{\partial(\ln(p))}{\partial a_j}\qquad \text{car :}\quad\Delta S=k~\ln(p)\]

Il vient donc:

\[\begin{aligned} &\overline{a_i~X_i}=k~\int...\int a_i~\frac{\partial(\ln(p))}{\partial a_j}~P~da_1~\dots~da_n\\ &\overline{a_i~X_i}=k~\int...\int da_1~\dots~da_{i\neq j}~\dots~da_n\int a_i~\frac{\partial P}{\partial a_j}~da_j \end{aligned}\]

En intégrant par parties en remarquant que \[\frac{\partial a_i}{\partial a_j}=\delta_i^j\qquad\text{(symbole de Kronecker)}\]

et que \(P\) s’annule aux limites du domaine de variation des \(a_i\), il vient : \[\overline{a_iX_j}=-k~\int...\int P~\delta_i^j~a_j\]

En remarquant que : \[\int...\int P(a_1,~\dots,~a_n)~da_1~\dots~da_n=1\]

On obtient : \[\overline{a_i~X_j}=-k~\delta_i^j\]

– Nous allons maintenant introduire mathématiquement la réversibilité microscopique de la façon suivante :

Nous associons dans le système, en équilibre macroscopique, la valeur \(a_i(t)\) d’un certain écart à l’instant \(t\) à la valeur \(a_j(t+\tau)\) d’un autre écart à un instant ultérieur et nous considérons la valeur moyenne du produit de ces deux écarts, soit : \[\overline{a_i(t)~a_j(t+\tau)}\qquad\tau~\text{fixe}\]

Si les fluctuations \(a_i\) et \(a_j\) étaient rigoureusement indépendantes, cette valeur moyenne serait nulle puisque identiques au produit des valeurs moyennes \(\overline{a_i}\) et \(\overline{a_j}\) qui sont nulles toutes deux, mais il y a une certaine corrélation entre ces écarts ; on peut par exemple imaginer qu’un écart momentané de températures entre deux parties d’un système amène, de préférence, au cours des instants immédiatement ultérieurs, un écart de concentrations d’un signe déterminé.

Il en résulte que la valeur moyenne \(\overline{a_i(t)~a_j(t+\tau)} \) n’est pas nulle.

Nous introduisons la réversibilité macroscopique en exprimant que le renversement du temps conduit encore à une séquence normale de fluctuations, c’est-à-dire qu’elle est régie par les mêmes lois et présentant par suite les mêmes corrélations entre écarts de natures diverses, soit : \[\overline{a_i(t)~a_j(t+\tau)}=\overline{a_i(t)~a_j(t-\tau)}\]

Ce qui peut encore s’écrire, en remarquant que la loi de séquence des fluctuations est irréversible au cours du temps (équilibre thermodynamique macroscopique), ce qui nous permet de changer l’origine des temps dans le second membre : \[\overline{a_i(t)~a_j(t+\tau)}=\overline{a_j(t)~a_i(t-\tau)}\]

Nous remarquons alors que la moyenne indiquée dans chacun des membres de cette relation peut être calculée de la façon suivante :

Nous commençons par choisir tous les instants où le système présente un ensemble d’écarts bien déterminés \(a_k\) (à \(da_k\) près) et nous notons à chaque fois la valeur de \(a_j\), \(\tau\) secondes plus tard. Nous prenons la moyenne de ces valeurs de \(a_j\), moyenne qui n’est pas nulle puisque nous avons choisi aux instants \(\tau\) une configuration déterminée du système. D’où il résulte que sa configuration aux instants \(t\) et \(t + \tau\) n’est plus complètement arbitraire.

Nous représentons cette moyenne par : \[[\overline{a_j(t+\tau)}]_{a_1(t),~\dots,~a_n(t)}\]

et nous la multiplions par une valeur bien déterminée de \(a_i(t)\), puis nous faisons varier de façon arbitraire la configuration de départ à l’instant \(t\), ce qui revient par exemple à choisir de façon arbitraire d’autres fluctuations de départ, et prenons la moyenne des valeurs obtenues pour les produits : \[a_i(t)~[\overline{a_j(t+\tau)}]_{a_1(t),~\dots,~a_n(t)}\]

Nous obtenons ainsi une moyenne générale qui est égale au premier membre de l’équation considérée plus haut, soit : Nous pouvons alors mettre l’équation initiale sous la forme : \[\overline{{a_i(t)~[\overline{a_j(t+\tau)}]}_{a_1(t),~\dots,~a_n(t)}}=\overline{{a_j(t)~[\overline{a_i(t+\tau)}]}_{a_1(t),~\dots,~a_n(t)}}\]

Soustrayons aux deux membres la même quantité \(\overline{a_i(t)~a_j(t)}\).

L’équation précédente devient : \[\overline{{a_i(t)~[\overline{a_j(t+\tau)-a_j(t)}]}_{a_1(t),~\dots,~a_n(t)}}=\overline{{a_j(t)~[\overline{a_i(t+\tau)-a_i(t)}]}_{a_1(t),~\dots,~a_n(t)}}\]

– Introduisons maintenant la troisième partie du raisonnement qui constitue une hypothèse :

Lorsque nous écartons délibérément le système de son état d’équilibre en donnant des valeurs notables aux \(a_i\), nous observons un retour spontané du système vers l’équilibre, avec une vitesse qui, pour des écarts pas trop importants, est proportionnel à l’écart résiduel.

Plus exactement, chaque écart \(a_i\) se réduit progressivement avec une vitesse : \[\frac{da_i}{dt}=a_i^0=J_i=\sum_k L_{ik}~X_k\]

Faisons la même expérience en imposant au système un ensemble d’écarts bien déterminés, mais extrêmement petits, du même ordre que ceux qui sont observés au cours des fluctuations spontanées. Il en résulte un ensemble de forces de rappel \(X_k\) bien déterminées et très faibles. Nous supposerons alors que, lorsque cet ensemble d’écarts bien déterminés est observé au cours des fluctuations, il se trouve accompagné d’un ensemble de vitesses de modification \(a_i^0\) qui, en moyenne, s’expriment de la même façon en fonction des \(X_k\), soit : \[\overline{a_i^0(t)}=L_{ik}~X_k(t)\]

Ce qui veut dire qu’après un intervalle de temps grand devant celui qui sépare deux chocs moléculaires, mais petit devant le temps nécessaire pour qu’un ensemble d’écarts soit sensiblement réduit, nous pourrons observer un ensemble d’écarts \(a_i(t+\tau)\) tels que (en moyenne pour beaucoup d’observations correspondant au même ensemble d’écarts initiaux \(a_k(t)\)) : \[a_j(t+\tau)-a_i(t)=\tau~\sum_k L_{ik}~X_k(t)\]

Comparons l’équation précédemment obtenue entre les valeurs moyennes ; il vient, en divisant par \(\tau\) : \[\overline{a_j(t)~\sum_k L_{ik}~X_k(t)}=\overline{a_i(t)~\sum_k L_{jk}~X_k(t)}\]

En remarquant que :

\[\begin{aligned} \overline{a_j~X_k}=-k~\delta_{jk}\quad&;\quad \overline{a_i~X_k}=-k~\delta_{ik}\\ -k~\sum_k L{ik}~\delta_{jk}&=-k~\sum_k L{jk}~\delta_{ik}\end{aligned}\]

On obtient bien les relations d’Onsager : \[L_{ij}=L_{ji}\]

5. Application : étude thermodynamique du thermocouple

Rappelons tout d’abord les faits expérimentaux qui caractérisent l(effet Seebeck ou effet thermoélectrique.

Nous constituons un thermocouple en connectant aux deux extrémités d’un conducteur \(A\) deux tronçons conducteurs \(B\) et \(B'\) formés d’un même métal \(B\) différent de celui qui constitue \(A\). Nous réunissons les deux extrémités libres des conducteurs \(B\) et \(B'\) aux bornes \(P\) et \(Q\) d’un millivoltmètre.

Maintenons les bornes \(P\) et \(Q\) à la même température et plongeons les deux soudures \(A-B\) et \(A-B'\) dans deux thermostats de températures différentes \(T\) et \(T+\Delta T\). Nous observons une déviation de l’aiguille du millivoltmètre, ce qui indique qu’une force électromotrice a pris naissance dans la chaîne de conducteurs. Cette force électromotrice s’annule avec \(\Delta T\). Le phénomène porte le nom d’effet thermoélectrique ou effet Seebeck.

Si la résistance du millivoltmètre est très grande devant celle du thermocouple, toute la f.é.m. thermoélectrique apparaît sous forme d’une différence de potentiel \[V_P-V_Q=E\qquad\text{f.é.m. du thermocouple}\]

Elle dépend de \(T\), de l’écart de température \(\Delta T\) entre les deux jonctions et de la nature des conducteurs \(A\) et \(B\).

5.1. Phénomènes dans le thermocouple

Pour appliquer la thermodynamique à l’étude de ce phénomène, nous commencerons par énumérer les divers phénomènes dont le thermocouple est le siège : effet Joule, conduction thermique, effet Peltier et effet Thompson.

5.1.1. Effet Joule

On sait qu’un courant électrique traduit un déplacement de porteurs de charges électriques dans un conducteur. Or, dans ce déplacement, ces porteurs interagissent avec les atomes du matériau qui deviennent un frein à ce déplacement. Aussi est-il nécessaire, pour transmettre une certaine quantité de courant électrique, de fournir une puissance supplémentaire qui sera dissipée sous forme d’énergie thermique lors de ces interactions.

L’effet Joule est ainsi la manifestation thermique de la résistance électrique.

5.1.2. Conduction thermique

La conduction (ou diffusion) thermique est un phénomène de transfert. Il est provoqué de manière naturelle par une différence de température entre deux régions d’un même milieu ou entre deux milieux mis en contact.

On peut l’interpréter comme la transmission de proche en proche d’une agitation thermique, un atome cédant une partie de son énergie cinétique à l’atome voisin.

5.1.3. Effet Peltier

L’effet thermoélectrique ou effet Peltier est un phénomène physique de déplacement de chaleur. Il est produit dans des matériaux conducteurs électriques de natures différentes en contact par des jonctions. L’une des jonctions se refroidit légèrement alors que l’autre se réchauffe.

Quand un courant \(i\) traverse dans le sens \(A\rightarrow B\) la jonction de deux métaux différents \(A\) et \(B\), maintenue à température constante par une source de chaleur, une certaine quantité de chaleur \(q\) est libérée par seconde dans la jonction, en plus de la chaleur produite par effet Joule.

Le maintien à température constante de la jonction par la source de chaleur exige donc que soit extraite à chaque seconde, en plus de la chaleur produite par effet Joule, une certaine quantité de chaleur supplémentaire (positive ou négative) \(q\).

Cette quantité de chaleur \(q\) porte le nom de chaleur Peltier.

Elle est proportionnelle à l’intensité \(i\) du courant qui traverse la jonction et change de signe quand on renverse le sens du courant, ce qui la distingue nettement de la chaleur produite par effet Joule. Suivant le sens du courant, l’effet Peltier se traduit donc par une absorption ou un dégagement de chaleur Peltier par la jonction.

Nous avons signalé que la chaleur Peltier est proportionnelle au courant \(i\) qui traverse la jonction dans le sens \(A\rightarrow B\). Le coefficient de proportionnalité \(\Pi\) dépend de la nature des deux métaux \(A\) et \(B\) et de la température \(T\) de la jonction. Nous pourrons le représenter par \(\Pi_{A-B}(T)\).

Nous conviendrons de compter positivement la chaleur Peltier lorsqu’elle est dégagée par la jonction et écrirons par suite, en désignant par \(i\) l’intensité (positive ou négative) qui circule dans le sens \(A\rightarrow B\) et par \(q\) la chaleur dégagée par la jonction (en plus de l’effet Joule)

Chaleur Peltier produite en 1 seconde : \[q=i~\Pi_{A-B}(T)\]

Chaleur Peltier produite pendant le temps dt : \[dq=i~dt~\Pi_{A-B}(T)\]

5.1.4. Effet Thomson

Soient deux points \(P\) et \(Q\) d’un même conducteur \(A\), maintenus respectivement aux températures \(T\) et \(T + dT\), par deux sources de chaleur. Tant qu’aucun courant ne traverse le conducteur, une certaine quantité de chaleur traverse l’élément de conducteur thermique \(PQ\) et passe donc d’une source à l’autre.

Faisons passer un courant \(i\) dans le conducteur ; une certaine quantité de chaleur est produite par effet Joule et passe dans les sources. En outre, le passage du courant entraîne, suivant le passage du courant, à chaque seconde, d’une quantité de chaleur supplémentaire qui porte le nom de chaleur de Thomson.

En d’autres termes, le maintient aux températures fixes \(T\) et \(T + dT\) des deux points \(P\) et \(Q\) du conducteur exige, lorsqu’un courant \(i\) le traverse dans un certain sens, le dégagement par l’ensemble des deux sources d’une quantité de chaleur qui comprend, d’une part la quantité de chaleur négative correspondant à l’effet Joule et qui ne dépend pas du sens de circulation du courant et d’autre part une quantité de chaleur supplémentaire, la chaleur Thomson, qui change de signe lorsqu’on inverse le sens de circulation du courant.

La chaleur Thomson est proportionnelle à l’intensité \(i\) du courant (en grandeur et en signe) et à l’écart de température \(dT\) entre les points \(P\) et \(Q\) ; nous conviendrons de désigner par la chaleur Thomson absorbée par le conducteur lorsque l’unité de charge traverse la section \(PQ\) dans le sens \([T,~T+dT]\).

Le passage du courant \(i\) entre les sections \(P\) et \(Q\) du conducteur de températures respectives \([T,~T+dT]\), entraîne donc par seconde l’absorption d’une chaleur Thomson : \[dq=\sigma_A~i~dT\]

Le coefficient de proportionnalité \(\sigma_A\) (coefficient Thomson) dépend de la nature du conducteur \(A\) et de sa température \(T\), soit : \[dq=\sigma_A(T)~i~dT\]

5.2. Impact des effets Peltier et Thompson

Nous allons tout d’abord voir, en appliquant le premier principe de la thermodynamique, comment l’effet Seebeck est lié aux effets Peltier et Thomson.

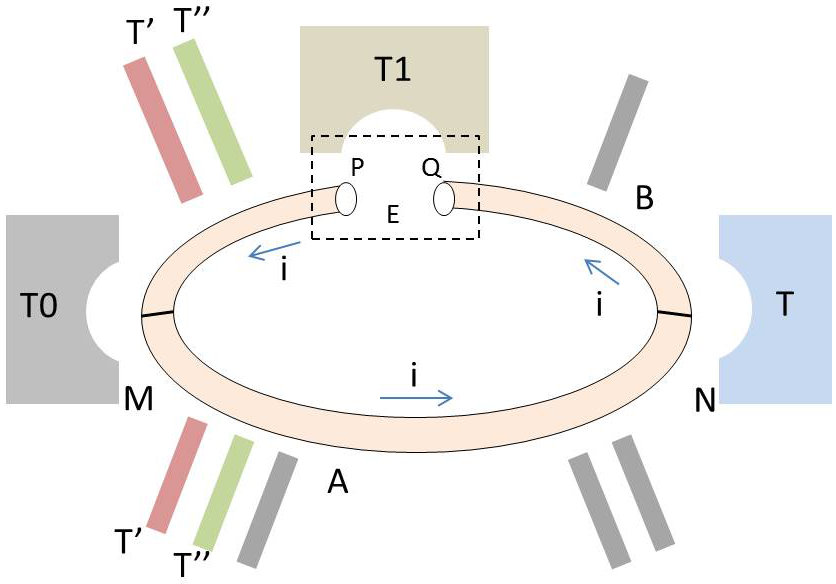Réalisons le montage ci-contre.

Les jonctions \(M\) et \(N\) sont maintenues aux températures fixes \(T_0\) et \(T\) par deux sources de chaleur.

Entre les points \(P\) et \(Q\) du conducteur \(B\) est intercalé un générateur de f.é.m. \(E\) qui fait circuler dans le thermocouple le courant \(i\) (compté positivement dans le sens de la flèche).

Nous supposons, pour fixer les idées, que le sens de branchement du générateur est tel que le courant \(i\) est de sens opposé à celui qui traverserait le thermocouple si on mettait en court-circuit les points \(P\) et \(Q\) (il faut évidemment que \(E\) soit assez important pour surpasser la f.é.m. du thermocouple qui joue le rôle d’une f.c.é.m.).

Nous supposons que l’ensemble du générateur et des bornes \(P\) et \(Q\) est maintenu par une source de chaleur à une température \(T_1\), intermédiaire entre \(T_0\) et \(T\). Enfin, chaque section des conducteurs est maintenue à température constante par une suite de sources de chaleur de températures échelonnées entre \(T_0\) et \(T\).

Un régime permanent s’établit ainsi ; à chaque seconde une certaine quantité de travail électrique \(E_i\) est transformée en chaleur qui se répartit entre les diverses sources.

Établissons le bilan énergétique pendant 1 seconde. La chaleur distribuée sur l’ensemble des sources du fait du passage du courant \(i\) comprend :

1. une chaleur de Joule \(R~i^2\) (\(R\) résistance totale de la chaîne, y compris la résistance interne du générateur) répartie sur l’ensemble des sources ;

2. la chaleur Peltier \(i~\Pi_{A\rightarrow B}(T)\) dégagée par la jonction \(N\) parcourue dans le sens \(A\rightarrow B\) par le courant \(i\) ;

3. la chaleur Peltier \(-i~\Pi_{A\rightarrow B}(T_0)\) dégagée par la jonction M parcourue dans le sens \(A\rightarrow B\) par le courant \((-i)\) ;

4. l’ensemble des chaleurs Thomson absorbées par les sources échelonnées, soit pour les sources en contact avec le conducteur \(A\) où le courant circule dans le sens \([T_0,~T]\) : \[q_A=-\int_{T_0}^T\sigma_A(T)~i~dT\]

Rappelons que c’est la chaleur absorbée par le conducteur que nous représentons par \((\sigma~i~dT)\) et, pour les sources en contact avec le conducteur \(B\) parcouru dans le sens \((T_0,~T)\) par le courant \((-i)\), : \[q_B=+\int_{T_0}^T \sigma_B(T)~i~dT\]

Au total, la chaleur absorbée en 1 seconde par l’ensemble des sources est : \[Q=R~i^2+i~\Pi_{A-B}(T)-i~\Pi_{A-B}(T_0)+i~\int_{T_0}^T (\sigma_B-\sigma_A)~dT\]

5.2.1. Première relation du thermocouple

La variation totale d’énergie de l’Univers est nulle, soit : \[-E_i+Q=0\quad;\quad E_i=Q\]

Ce qui s’écrit, en divisant par \(i\) : \[E'=R~i=\Pi_{A-B}(T)-\Pi_{A-B}(T_0)+\int_{T_0}^T (\sigma_B-\sigma_A)~dT\]

Abaissons la f.é.m. du générateur jusqu’à annuler exactement le courant \(i\) : \(E'\) est alors exactement égale à la f.é.m. du thermocouple. Nous pouvons alors en déduire la valeur de la f.é.m. du thermocouple : \[\mathcal{E}(T,~T_0)=\Pi_{A-B}(T)-\Pi_{A-B}(T_0)+\int_{T_0}^T (\sigma_B-\sigma_A)~dT\]

C’est la première relation du thermocouple. On l’écrit souvent en considérant que la soudure \(M\) est placée à une température \(T_0\) fixe (par exemple glace fondante) et la soudure \(N\) à une température \(T\) variable.

La variation \([T\rightarrow T+dT]\) de la température de \(N\) entraîne une variation \(dE\) de la f.é.m. du thermocouple, donnée par dérivation de la formule ci-dessus : \[\frac{d\mathcal{E}}{dT}=\frac{d(\Pi_{A-B})}{dT}+(\sigma_B-\sigma_A)\]

C’est la première loi du thermocouple.

Il convient de remarquer ici que l’expression que nous avons obtenue pour \(\mathcal{E}(T,~T_0)\) nous permet d’écrire immédiatement : \[\mathcal{E}(T',~T_0)=\mathcal{E}(T',~T)+\mathcal{E}(T,~T_0)\]

Ce qui revient à dire que le rapport \(d\mathcal{E}/dT\) peut s’interpréter de deux façons différentes :

1. soit comme la dérivée par rapport à \(T\) de la f.é.m. d’un thermocouple dont la soudure froide est à une température fixe \(T_0\) et la soudure chaude à la température variable \(T\) ;

2. soit comme le quotient par \(dT\) de la f.é.m. \(d\mathcal{E}\) d’un thermocouple dont la soudure froide est à la température \(T\) et la soudure chaude à la température \(T+dT\).

Nous allons utiliser cette remarque dans ce qui va suivre pour chercher une seconde expression de \(d\mathcal{E}/dT\).

5.2.2. Seconde relation du thermocouple

Nous considérons un thermocouple dont les soudures sont aux températures extrêmement voisines \(T~;~T+\delta T\) et cherchons à obtenir une expression de sa f.é.m. \(\delta\mathcal{E}\) en appliquant les relations d’Onsager. Le quotient \(\delta\mathcal{E}/\delta T\) obtenu sera identique à la dérivée \(d\mathcal{E}/dT\). L’expression obtenue constituera la deuxième loi du thermocouple.

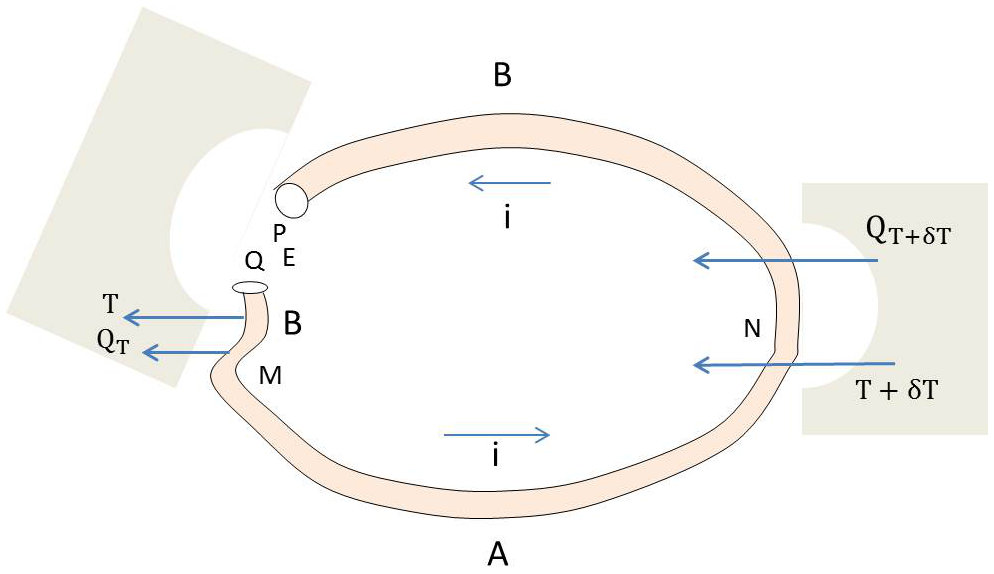Nous réalisons dans ce but le montage ci-contre.

Le générateur et la jonction \(M\) sont mis en contact thermique avec le thermostat de température \(T\) (les points \(P\), \(Q\) et \(M\) sont notamment à la température \(T\)).

La jonction \(N\) est mise en contact thermique avec un thermostat de température . Le reste des conducteurs \(A\) et \(B\) est isolé thermiquement sur ses faces latérales.

L’ensemble des deux thermostats et du générateur constitue donc avec le thermocouple un système isolé dont l’entropie totale ne peut aller qu’en croissant.

Au bout d’un temps plus ou moins long après que la f.é.m. du générateur ait été réglée à la valeur fixe \(\delta E\), un régime permanent d’écoulement de charges et de chaleur s’établit. Chaque point du thermocouple se maintient à température constante et l’état du thermocouple reste stationnaire, donc d’entropie constante.

Le générateur que nous supposerons par exemple actionné par la descente de poids et dépourvu de frottements, garde une entropie constante. La variation d’entropie du système isolé se réduit donc à la variation totale d’entropie de l’ensemble des deux sources de chaleur.

Désignons par \(Q_T\) la chaleur qui pénètre en 1 seconde dans la source \(T\) et par \(Q_{T+\delta T}\) celle qui quitte en 1 seconde la source.

La variation d’entropie totale en 1 seconde, c’est-à-dire la vitesse \(\Delta S\) d’accroissement de l’entropie est donc : \[\Delta S=\frac{Q_T}{T}-\frac{Q_{T+\delta T}}{T+\delta T}\]

Ce que nous pouvons écrire : \[\Delta S=Q_T~\Big(\frac{1}{T}-\frac{1}{T+\delta T}\Big)+\frac{1}{T+\delta T}~(Q_T-Q_{T+\delta T})\]

Le premier principe nous apprend que, si l’intensité qui traverse le thermocouple est \(i\) : \[i~\delta E=Q_T-Q_{T+\delta T}\]

Il vient donc : \[\Delta^0S=Q_T~\frac{\delta T}{T~(T+\delta T)}+i~\frac{\delta E}{T+\delta T}\]

Supposons alors que \(dE\), quoique étant un peu supérieur à la f.c.é.m. \(\delta\mathcal{E}\) du thermocouple, est du même ordre de grandeur.

Les quantités \(i,~Q_T,~\delta\mathcal{E},~\delta T\) sont alors du même ordre qui est celui de \(\delta T\).

Les deux termes qui figurent dans l’expression de \(\Delta^0S\) sont de l’ordre de \((\delta t)^2\) et nous ne ferons qu’une erreur du \(3^o\) ordre, donc négligeable, en remplaçant dans les deux dénominateurs \(T+\delta T\) par \(T\). Il vient alors : \[\Delta^0S=Q_T~\frac{\delta T}{T^2}+i~\frac{\delta E}{T}\]

\(Q_T\) a les dimensions d’un flux de chaleur (chaleur pénétrant par seconde dans la source \(T\)) et l’intensité \(i\) a les dimensions d’un flux de charges électriques. Nous écrirons alors : \[\Delta S=J_1~X_1+J_2~X_2\]

associant respectivement aux flux :

\[\begin{aligned} &J_1=Q_T &&\text{flux de chaleur}\\ &J_2=i &&\text{flux de charges}\end{aligned}\]

les forces :

\[\begin{aligned} &X_1=\frac{\delta T}{T^2} &&\text{force associée au déséquilibre thermique}\\ &X_2=\frac{\delta E}{T} &&\text{force associée au déséquilibre électrique}\end{aligned}\]

Suivant la méthode générale d’étude des phénomènes irréversibles couplés, nous écrirons alors les relations phénoménologiques :

\[\begin{aligned} &J_1=Q_T=L_{11}~\frac{\delta T}{T^2}+L_{12}~\frac{\delta E}{T}\\ &J_2=i=L_{21}~\frac{\delta T}{T^2}+L_{22}~\frac{\delta E}{T}\end{aligned}\]

Le théorème d’Onsager nous permet alors d’écrire : \[L_{12}=L_{21}\]

Nous allons maintenant chercher la signification physique des relations phénoménologiques en considérant deux cas particuliers de régime stationnaire pour le thermocouple.

Premier Cas

Nous réglons \(dE\) de façon à équilibrer exactement la f.c.e.m. du thermocouple. Nous aurons alors : \[i=0\quad;\quad\delta E=\delta\mathcal{E}\]

La seconde relation phénoménologique s’écrit alors : \[L_{21}~\frac{\delta T}{T^2}+L_{22}~\frac{\delta\mathcal{E}}{T}\quad\Rightarrow\quad\frac{\delta\mathcal{E}}{T}=-\frac{1}{T}~\frac{L_{21}}{L_{22}}\]

La relation obtenue est caractéristique de l’effet Seebeck ou effet thermoélectrique (apparition en circuit ouvert d’une f.é.m. \(\delta\mathcal{E}\) proportionnelle à l’écart de température \(\delta T\)).

Deuxième cas

Nous plaçons les deux jonctions à la même température \(T\), soit \(\delta T = 0\).

Faisons passer un courant \(i\) dans le thermocouple au moyen de la f.é.m. \(\delta E\).

Il en résulte un écoulement de chaleur dans la source de gauche, bien que les deux sources soient à la même température. On peut aisément vérifier que cet écoulement de chaleur correspond à l’effet Peltier. En effet, nous pouvons tout d’abord observer que le courant \(i\) est de l’ordre de grandeur \(\delta\mathcal{E}\), et que la chaleur Peltier \([-i~\Pi_{A-B}(T)]\) est donc du même ordre de grandeur.

D’autres causes peuvent cependant faire pénétrer dans la source \(T\) un supplément de chaleur. En effet, une partie de la chaleur de Joule produite tout au long du circuit pénètre dans la source \(T\), mais cette chaleur de Joule est proportionnelle à \(i^2\), donc du second ordre.

Par ailleurs, de petites différences de températures peuvent se produire dans le voisinage de la jonction \(M\), en vertu de l’effet Joule, et entraîner l’apparition de chaleur Thomson, mais les différences de température sont de l’ordre de l’énergie produite par effet Joule, donc de l’ordre de \(i^2\) et les chaleurs Thomson sont donc du troisième ordre. Nous pourrons donc négliger ces chaleurs additionnelles et considérer que la chaleur \(Q_T\) se réduit lorsque \(\delta T = 0\) à la chaleur Peltier.

L’effet Peltier se déduit alors des deux relations phénoménologiques lorsqu’on y fait \(\delta T=0\) : \[\frac{Q_T}{i}=-\Pi_{A-B}=\frac{L_{12}}{L_{22}}\]

C’est-à-dire encore : \[\Pi_{A-B}=-\frac{L_{12}}{_{L22}}\]

Comparons les relations obtenues dans les deux cas en appliquant la relation d’Onsager. Il vient : \[\frac{\Pi_{A-B}}{T}=\frac{\delta\mathcal{E}}{\delta T}\]

D’où la seconde relation du thermocouple : \[\frac{\delta\mathcal{E}}{\delta T}=\frac{\Pi_{A-B}(T)}{T}\]

Nous pouvons y considérer le quotient du premier ordre comme la dérivée par rapport à \(T\) de la f.é.m. \(\mathcal{E}\) d’un thermocouple dont la soudure est maintenue à la température fixe \(T_0\), la soudure étant à la température variable \(T\).

5.2.3. Synthèse

Nous avons alors les deux lois du thermocouple :

\[\begin{aligned} &\frac{\delta\mathcal{E}}{\delta T}=\frac{\Pi_{A-B}(T)}{T}\\ &\frac{\delta\mathcal{E}}{\delta T}=\frac{d[\Pi_{A-B}(T)]}{dT}+\sigma_B-\sigma_A\end{aligned}\]

Nous pouvons écrire : \[\frac{d(\Pi_{A-B})}{dT}=d\Big(T~\frac{d\mathcal{E}}{dT}\Big)=\frac{d\mathcal{E}}{dT}+T~\frac{d^2\mathcal{E}}{dT^2}=\frac{d\mathcal{E}}{dT}+\sigma_A-\sigma_B\]

D’où il vient : \[T~\frac{d^2\mathcal{E}}{dT^2}=\sigma_A-\sigma_B\]

En définitive, les deux lois du thermocouple peuvent s’écrire :

\[\begin{aligned} \frac{\delta\mathcal{E}}{\delta T}&=\frac{\Pi_{A-B}(T)}{T}\\ T~\frac{d^2\mathcal{E}}{dT^2}&=\sigma_A-\sigma_B\end{aligned}\]

La première est assez bien vérifiée par l’expérience. La seconde l’est beaucoup moins.