1. Introduction et énoncés

Le premier principe nous a appris qu’un système passant d’un état initial \(I\) à un état final \(F\) en recevant du milieu extérieur un travail \(W\) (sous entendu mécanique) reçoit de ce milieu extérieur une chaleur \(Q\) telle que : \[U_F-U_I=W+Q\]

La différence \(U_F-U_I\) ne dépend que de l’état initial et de l’état final de système.

On pourrait imaginer mathématiquement la transformation inverse en écrivant : \[U_F-U_I=(-W)+(-Q)\]

1.1. Énoncé général

Si cette évolution inverse était possible (même s’agissant d’une transformation réversible), nous pourrions donc considérer qu’elle ramène aussi à son état initial le milieu extérieur et finalement une modification de l’Univers. Chose totalement impensable qui conduit à l’énoncé suivant :

• Un système isolé qui a subi une évolution ne peut plus revenir à son état initial.

Nous entendons par là que, cette évolution étant une évolution réelle, le système ne peut revenir à son état initial par une transformation réelle, ni même réversible.

1.2. Énoncé de Clausius

• Il est impossible de construire une machine qui, opérant suivant un cycle de transformations, n’ait produit au cours du cycle d’autre effet que le transfert d’une certaine quantité positive de chaleur d’un corps froid à un corps chaud.

Ceci est impossible, même pour une machine idéale qui fonctionnerait de façon irréversible.

1.3. Énoncé de Kelvin

• Il est impossible de construire une machine qui, opérant suivant un cycle de transformations, n’ait produit à la fin du cycle d’autre effet que l’extraction d’une quantité de chaleur positive d’une source unique et la production d’un travail positif (même en opérant de façon réversible).

On peut démontrer facilement que ces trois énoncés sont rigoureusement équivalents : l’affirmation de l’un d’entre eux permet de démontrer les autres.

1.4. Remarques

Les premier et deuxième principes de la thermodynamique interdisent toute forme de mouvement perpétuel.

Le premier s’oppose à la construction d’une machine qui fournirait indéfiniment du travail sans prendre d’énergie nulle part (mouvement perpétuel de première espèce).

Le second s’oppose à la construction d’une machine qui fournirait indéfiniment du travail en décrivant une suite indéfinie de cycles au cours desquels elle n’emprunterait d’énergie, sous forme de chaleur qu’à une seule source (mouvement perpétuel de seconde espèce).

2. Transformations monothermes

Nous désignerons par transformation monotherme toute transformation d’un système thermodynamique au cours de laquelle le système n’a échangé de chaleur qu’avec une seule source.

2.1. Cycles monothermes

Théorème 1

• Au cours d’un cycle de transformations monothermes d’un système quelconque, le système ne peut fournir au milieu extérieur un travail positif ; il reçoit donc du milieu extérieur un travail positif ou nul.

Supposons alors que le cycle de transformations monothermes soit en outre réversible. Faisons décrire ce cycle au système dans un sens donné : il reçoit du milieu extérieur le travail \(W\geq 0\) .

Faisons-lui maintenant décrire le même cycle en sens inverse : il reçoit le travail \([-W]\) et nous devons encore écrire \(W\geq 0\).

Ceci n’est possible que si \(W = 0\).

Théorème 2

• Au cours d’un cycle de transformations monothermes et réversible d’un système quelconque, le travail total reçu par le système du milieu extérieur est nul.

Il est vrai que, pratiquement, nous ne pouvons pas réaliser un cycle de transformations réversible, mais nous pouvons nous en approcher indéfiniment. Nous pourrons alors affirmer qu’un cycle décrivant un cycle monotherme infiniment voisin d’un cycle monotherme réversible reçoit au total un travail infiniment petit.

Du fait que le travail total reçu au cours d’un cycle monotherme et réversible est nul, nous déduisons immédiatement que la chaleur totale reçue \(Q\) l’est également.

En effet, puisqu’il s’agit d’un cycle \(W+Q=0\) .

Pour un cycle monotherme réel, nous avons toujours \(W+Q=0\), et, du fait que \(W>Q\) (cycle irréversible), nous tirons \(Q<0\).

2.2. Transformations monothermes non fermées

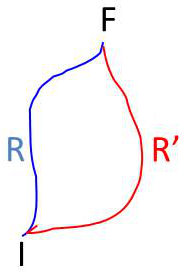Le système passe d’un état initial \(I\) à un état final\( F\) par une transformation monotherme réversible schématisée par la courbe \(IRF\).

Supposons une autre transformation monotherme réversible \(IR’F\). On peut donc imaginer que le système décrive un cycle monotherme réversible \(IRFR’I\). Il reçoit dans ce cas un travail total nul et une chaleur totale nulle.

On peut donc écrire : \[W_{IRF}+W_{FR'I}=0\qquad\text{et}\qquad Q_{IRF}+Q_{FR'I}=0\]

Comme les deux transformations sont inverses : \[W_{FR'I}=-W_{IR'F}\qquad\text{et}\qquad Q_{FR'I}=-Q_{IR'F}\]

On en tire : \[W_{IR'F}=W_{IRF}\qquad\text{et}\qquad Q_{IR'F}=Q_{IRF}\]

Ceci quel que soit le chemin monotherme et réversible \(IR’F\) que l’on puisse imaginer.

Nous l’exprimerons ainsi :

• Dans une transformation monotherme et réversible d’un système en relation avec une source de chaleur donnée, le travail reçu par le système est indépendant du chemin suivi et ne dépend que de l’état initial et de l’état final occupés par le système.

Pour qu’une transformation monotherme soit réversible, il faut notamment que le système soit constamment en équilibre. Ceci implique que, lorsqu’il échange effectivement de la chaleur avec la source et se trouve donc séparé d’elle par une cloison diatherme, il soit à la température de la source.

Un cas important de transformations monothermes réversibles est donc celui des transformations isothermes réversibles où le système garde constamment la température de la source.

On peut toutefois imaginer que le système quitte au cours de la transformation la température de la source. Il faut qu’il soit alors isolé de la source par une cloison adiabatique pour que son équilibre puisse subsister.

Une transformation monotherme réversible ne peut donc être constituée que d’une succession de transformations isothermes réversibles ayant toutes lieu à la même température (celle de la source), éventuellement entrecoupées de transformations adiabatiques réversibles.

Notons tout de suite que toutes les transformations monothermes et réversibles que nous considérerons seront des transformations isothermes. Il nous suffira donc d’exprimer le résultat obtenu sous la forme plus restrictive :

Dans toute transformation isotherme et réversible d’un système quelconque, le travail total reçu par le système est indépendant du chemin suivi et ne dépend que de l’état initial et de l’état final. Le premier principe exige alors qu’il en soit de même de la chaleur reçue par le système.

Suivant un raisonnement en tous points analogue à celui suivi pour l’introduction de l’énergie interne, nous retiendrons pour le moment que le travail \(dW\) reçu par le système dans une transformation élémentaire isotherme et réversible, est égal à la différentielle d’une certaine fonction \(F\). Cette différentielle est donc une différentielle totale exacte et si \(dW\) est mis sous la forme : \[dW=X~dx+Y~dy+Z~dz +\dots\]

nous pourrons écrire : \[\frac{\partial X}{\partial y}=\frac{\partial Y}{\partial x}\quad;\quad \frac{\partial X}{\partial z}=\frac{\partial Z}{\partial x}\quad;\quad\dots\]

Insistons sur le fait que ceci n’est vrai que si la transformation élémentaire est une transformation isotherme et réversible.

3. Transformations mettant en jeu deux sources de chaleur

Considérons maintenant une transformation cyclique d’un système quelconque au cours de laquelle le système a pu échanger de la chaleur avec deux sources distinctes, c’est-à-dire à températures différentes. Nous allons voir que, dans ces conditions, le second principe ne s’oppose plus à ce que le système ait, à la fin du cycle, fourni à l’extérieur un travail positif.

Le système revenant à son état initial à la fin du cycle, seul est modifié le milieu extérieur. Pour fixer les idées, désignons par \(C_1\) et \(C_2\) les deux sources de chaleur, \(C_1\) désignant la plus chaude des deux sources, et examinons en détail les modifications subies par le milieu extérieur à la fin du cycle qu’a décrit le système :

• Le système a reçu le travail total \(W\) ; ceci peut se ramener à l’abaissement d’un poids dans le milieu extérieur (abaissement positif si \(W\) est positif).

• La source chaude \(C_1\) a cédé la chaleur \(Q_1\) (au système).

• La source froide \(C_2\) a fourni la chaleur \(Q_2\) (au système).

Ce sont là les seules modifications du milieu extérieur entraînées par le cycle de transformations, et même les seules modifications de l’Univers entier, puisque le système est revenu en définitive à son état initial.

Au point de vue de son action sur le milieu extérieur, le cycle peut donc être défini par la seule connaissance de \(Q_1\) et de \(Q_2\), puisque \(W\) s’en déduit par application du Premier Principe : \[W+Q_1+Q_2=0\]

Nous pouvons dès lors représenter l’ensemble des modifications de l’Univers représentant un cycle de transformations considérées par un diagramme \([Q_1,Q_2]\), dit diagramme de Raveau.

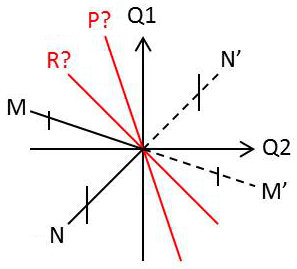Nous désignerons sous le nom de cycle, toute transformation portant sur un ou plusieurs systèmes et ramenant en définitive ce ou ces systèmes à leur état initial.

Nous dirons qu’un cycle est représenté par un point \(M\) du diagramme de Raveau lorsque les coordonnées de \(M\) représentent les effets du cycle sur le milieu extérieur.

Le second principe nous apprend alors qu’il est impossible d’effacer exactement les effets sur le milieu extérieur d’un cycle de transformations effectivement décrit par le système.

Nous en déduisons immédiatement que si le point \(M\) de coordonnées \([Q1, Q2]\) représente un cycle de transformations réel, le point \(M'\) de coordonnées \([-Q1, -Q2]\) ne peut correspondre à un cycle de transformations réel, portant sur le même système ou sur un ou plusieurs systèmes différents, car un tel cycle effacerait les effets du premier principe (le travail reçu par le système y serait \((-W)\) d’après le premier principe).

Par contre, tous les points de coordonnées \([\lambda~Q_1,~\lambda~Q_2]~;~\lambda >0]\) correspondent à des cycles effectivement réalisables (il suffit de multiplier par \(\lambda\) la masse du système qui a décrit le cycle \([Q_1, Q_2]\) et de lui faire décrire un cycle identique).

Tous les points de la demi-droite \(OM\) correspondent donc à des cycles réels, c’est-à-dire effectivement réalisables, tous les points de la demi-droite opposée \(OM'\) à des cycles irréalisables (même de façon irréversible).

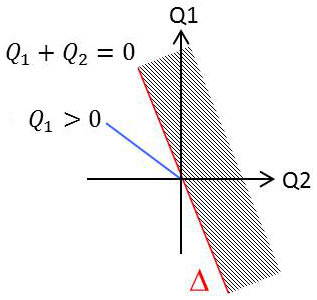On démontre, de proche en proche et par une technique de combinaisons linéaires le théorème suivant :

• Tous les points représentatifs des cycles réversibles décrits par un système quelconque qui n’échange de chaleur qu’avec \(C_1\) et \(C_2\) sont alignés sur une même droite \(\Delta\), dite droite des cycles réversibles.

En d’autres termes, \(Q_1 / Q_2\) est indépendant du système choisi et de la nature du cycle réversible qu’il décrit : il ne dépend que des sources \(C_1\) et\( C_2\).

Remarque

Deux sources de chaleur ne doivent être considérées comme distinctes que si elles sont à une température différente ; une source de chaleur se trouve donc entièrement définie au point de vue thermodynamique par la seule connaissance de sa température. Nous en déduisons que le rapport \(Q_1 / Q_2\) ne dépend que des températures \(T_1\) et \(T_2\) des deux sources \(C_1\) et \(C_2\).

Nous écrirons donc : \[\frac{Q_1}{Q_2}=f(T_1,~T_2)\]

Nous ignorons, pour le moment, la forme de la fonction \(f\).

4. Cycles réels

Tous les points représentatifs des cycles réels sont situés d’un même coté de la droite \(\Delta\).

On démontre que tous les points des demi-axes \([Q_2=0~;~Q_1<0]\) et \([Q_1=0~;~Q_2<0]\) sont du coté des cycles réels. Tous les points situés au dessus de cette droite correspondent à des cycles irréalisables.

5. Température thermodynamique

Nous avons vu qu’un système qui décrit un cycle réversible en n’empruntant de chaleur qu’à deux sources \(C_1\) et \(C_2\) reçoit de ces deux sources, au cours du cycle, des quantités de chaleur \(Q_1\) et \(Q_2\) dont le rapport ne dépend que des températures \(T_1\) et \(T_2\) des deux sources, soit : \[\frac{Q_1}{Q_2}=f(T_1,~T_2)\]

Envisageons alors trois sources de chaleur \(C_1,~C_2,~C_3\) aux températures \(T_1,~T_2,~T_3\) et des cycles réversibles décrits par un système quelconque n’échangeant de chaleur qu’avec deux de ces sources (nous dirons que le cycle est décrit entre les deux sources qui échangent de la chaleur avec le système).

Faisons décrire au système un premier cycle réversible entre \(C_1\) et\(C_3\). Il reçoit de ces deux sources les quantités de chaleur \(Q_1\) et \(Q_3\). Nous avons : \[\frac{Q_1}{Q_3}=f(T_1,~T_3)\]

Faisons maintenant décrire au système un cycle réversible entre \(C_2\) et \(C_3\), au cours duquel il reçoit la quantité de chaleur \((-Q_3)\) de la source \(C_3\). Il reçoit dès lors de \(C_2\) une quantité de chaleur \(Q_2\) telle que : \[\frac{Q_2}{-Q_3}=f(T_2,~T_3)\]

L’ensemble de ces deux cycles peut être considéré comme un cycle réversible décrit entre \(C_1\) et \(C_2\), puisqu’au total \(C_3\) a fourni la quantité de chaleur \(Q_3-Q_3=0\). Nous avons donc : \[f(T_1,~T_2)=\frac{Q_1}{Q_2}=\frac{Q_1}{Q_3}\times\frac{Q_3}{Q_2}=-\frac{f(T_1,~T_3)}{f(T_2,~T_3)}\]

Nous pourrons alors supposer \(T_3\) fixe et \(T_1\) et \(T_2\) variables. Nous poserons donc : \[f(T_1,~T_3)=\psi(T_1)\qquad;\qquad f(T_2,~T_3)=\psi(T_2)\]

Ce qui entraine : \[f(T_1,~T_2)=-\psi(T_1)~\psi(T_2)\]

La forme de la fonction \(\Psi\) dépend de la température \(T_3\) choisie, mais le rapport \(\psi(T_1)/\psi(T_2)\) n’en dépend pas.

Faisant choix d’une autre température \(T'_3\) pour la source \(C_3\), nous aurions obtenu une autre fonction \(\phi\) avec :

\[\begin{aligned} &\frac{\varphi(T_1)}{\varphi(T_2)}=-f(T_1,~T_2)=\frac{\psi(T_1)}{\psi(T_2)}\\ &\frac{\varphi(T_1)}{\psi(T_1)}=\frac{\varphi(T_2)}{\psi(T_2)}=~cte~=k\end{aligned}\]

puisque \(T_1\) et \(T_2\) sont quelconques.

Quel que soit \(T\), on a donc : \[\varphi(T)=k~\psi(T)\]

Le fait de changer la température de la source \(C_3\) revient donc à multiplier par une constante la fonction \(\psi\).

Cette fonction est donc définie à une constante multiplicative près par la relation : \[f(T_1,~T_2)=-\frac{\psi(T_1)}{\psi(T_2)}\]

Par définition, nous désignons par température thermodynamique d’une source \(C\) à la température absolue \(T\) la quantité \(\theta=\psi(t)\).

Remarquons que l’échelle de température ainsi définie ne l’est qu’à une constante multiplicative près ; il suffira pour définir complètement l’échelle de fixer arbitrairement la température thermodynamique d’un seul point fixe, par exemple le point triple de l’eau (équilibre eau – glace – vapeur).

D’ores et déjà, le rapport des températures thermodynamiques de deux sources prend une signification intrinsèque, non rattachée comme c’était le cas pour la température absolue aux propriétés d’un corps particulier tel que le gaz parfait :

• Le rapport des températures thermodynamiques de deux sources de chaleur est égal, au signe près, au rapport constant des quantités de chaleur que fournissent ces sources à un système quelconque qui décrit un cycle réversible en n’échangeant de chaleur qu’avec elles.

6. Identification des températures thermodynamique et absolue

Pour établir expérimentalement la valeur du rapport des températures thermodynamiques de deux sources de chaleur on fait décrire à un système bien déterminé un cycle réversible entre ces deux sources et on mesure les quantités de chaleur qu’il reçoit des deux sources au cours du cycle.

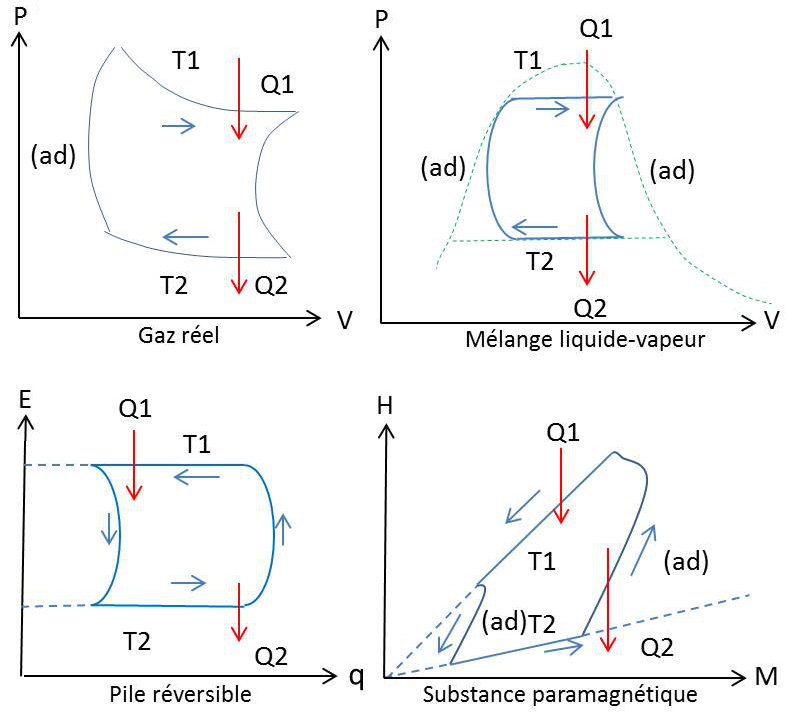Un cycle particulièrement intéressant est celui du cycle de Carnot.

Pour que l’échange de chaleur entre le système entre le système et une source soit réversible, il faut que le système soit à l’équilibre thermique avec la source, donc qu’il soit à la température de la source.

Toute portion du cycle où le système échange effectivement de la chaleur avec une des deux sources doit donc être un isotherme pour que ce cycle soit réversible.

Il faut bien toutefois que le système passe à moment donné de la température d’une source à celle de l’autre source, pour pouvoir échanger de manière réversible de la chaleur avec les deux sources au cours du cycle.

Au cours de ce passage de la température \(T_1\) à la température \(T_2\), le système ne doit échanger de chaleur avec aucune des deux sources. Sa transformation doit être adiabatique.

Le cycle le plus simple qui satisfasse à la condition de réversibilité et au cours duquel le système échange effectivement de la chaleur avec les deux sources est donc composé de deux arcs d’isothermes, aux températures \(T_1\) et \(T_2\) des deux sources, arcs dont les extrémités sont joints par deux arcs d’adiabatiques.

Un tel cycle porte le nom de cycle de Carnot, du nom du jeune ingénieur français Sadi-Carnot (1824) qui décrivit ce système avec la machine de Carnot.

6.1. Cycle de Carnot d’une mole de gaz parfait

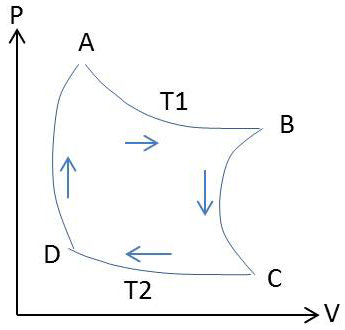Dans le diagramme de Clapeyron, le cycle sera représenté par la succession de l’isotherme \(AB\) (\(T_1\) : température de \(C_1\)), de l’adiabatique réversible \(BC\), de l’isotherme \(CD\) (\(T_2\) : température de \(C_2\)) et enfin de l’adiabatique \(DA\) (réversible).

Dans ces diverse transformations réversibles, les quantités de chaleur reçues par la mole de gaz parfait considérée sont :

• dans \(AB\), chaleur reçue (de \(C_1\)) = \(Q_{A~\rightarrow~B}\) ;

• dans \(BC\), chaleur reçue = 0 ;

• dans \(CD\), chaleur reçue (de \(C_2\)) = \(Q_{C~\rightarrow~D}\) ;

• dans \(AD\), chaleur reçue = 0.

Le cycle étant réversible, nous poserons par définition : \[\frac{Q_{A\rightarrow} B}{Q_{C\rightarrow} D}=f(T_1,~T_2)=-\frac{\psi(T_1)}{\psi(T_2)}=-\frac{\theta_1}{\theta_2}\]

Comme l’énergie interne d’un gaz parfait ne varie pas dans une transformation isotherme, nous avons :

\[\begin{aligned} &Q_{A\rightarrow B}=-W_{A\rightarrow B}=R~T_1~\ln\frac{v_A}{v_B}\\ &Q_{C\rightarrow D}=-W_{C\rightarrow D}=R~T_2~\ln\frac{v_D}{v_C}\end{aligned}\]

Nous en tirons : \[\frac{\theta_1}{\theta_2}=-\frac{T_1}{T_2}=\ln\frac{v_B/v_A}{v_D/v_C}\]

Remarquons alors que \(BC\) et \(DA\) sont des adiabatiques réversibles qui, le gaz étant parfait, sont régies par des équations dont l’une des formes (suivant la nature du gaz) a pour expression : \[v~T^{1/\gamma-1}=cte\]

\(\gamma\) désignant le rapport des capacités calorifiques à pression constante et à volume constant.

Nous avons donc : \[\frac{v_B}{v_C}=\Big(\frac{T_1}{T_2}\Big)^{1/1-\gamma}\qquad \text{c'est-à-dire :}\quad\frac{v_B}{v_A}=\frac{v_C}{v_D}\]

Il vient donc : \[\frac{\ln(v_B/v_A)}{\ln(v_D/v_C)}=-1\qquad\Rightarrow\qquad\frac{\theta_1}{\theta_2}=\frac{T_1}{T_2}\]

Le rapport des températures thermodynamiques des deux sources est donc égal au rapport de leurs températures absolues. Les deux échelles de températures sont donc proportionnelles.

Nous avons vu précédemment que notre définition laissait arbitraire un coefficient multiplicatif pour la température thermodynamique. Nous fixerons ce coefficient en posant par définition que la température thermodynamique \(\theta\) du point triple est égale à sa température \(T_0\) = 273,16 °C. Nous assurons ainsi sur l’ensemble des échelles de température une identité complète entre la température thermodynamique \(\theta\) et la température absolue \(T\).

Nous aurons donc \(\theta=T\) et nous pourrons désigner par \(T\) la température thermodynamique d’une source aussi bien que sa température absolue. La température thermodynamique sera exprimée en kelvins (symbole : K).

7. Caractéristiques du diagramme de Raveau

Soient \(T_1\) et\(T_2\) les températures thermodynamiques des sources \(C_1\) et \(C_2\) ; pour tout cycle réversible d’un système quelconque n’empruntant de chaleur qu’à ces deux sources, nous pourrons écrire : \[\frac{Q_1}{Q_2}=-\frac{T_1}{T_2}\]

L’équation de la droite \(\Delta\) des cycles réversibles est donc : \[\frac{Q1}{T1}+\frac{Q2}{T2}=0\]

Les cycles réels sont par contre représentés par des points au-dessous de la droite \(\Delta\) : \[\frac{Q1}{T1}+\frac{Q2}{T2}<0\]

Ces relations sont symétriques en \(T_1\) et \(T_2\). Elles restent les mêmes quelles que soient les températures des deux sources. \(C_1\) peut, par exemple, être la source froide aussi bien que la source chaude. Pour pouvoir étudier les caractéristiques des diverses régions du diagramme, nous continuerons cependant à supposer que \(C_1\) est la source la plus chaude, soit \(T_1 > T_2\).

Rappelons qu’au cours d’un cycle représenté par le point \([Q_1,~Q_2]\) le système reçoit du milieu extérieur un travail total \(W=-(Q_1+Q_2)\).

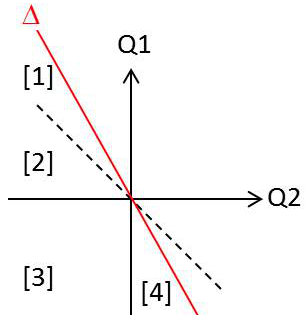Partageons en quatre régions la région des cycles réels, comme indiqué sur la figure.

– Dans la région [1] :

\[\begin{aligned} &Q_1+Q_2>0\qquad\Rightarrow\qquad W<0\\ &Q_1>0\quad;\quad Q_2<0\quad;\quad|Q_1|>|Q_2|\end{aligned}\]

Au cours du cycle, le système reçoit de la chaleur de la source chaude et en restitue une partie à la source froide, tout en fournissant du travail au milieu extérieur. Le système constitue donc une machine thermique.

– Dans la région [2] :

\[\begin{aligned} &Q_1+Q_2<0\qquad\Rightarrow\qquad W>0\\ &Q_1>0\quad;\quad Q_2<0\quad;\quad|Q_2|>|Q_1|\end{aligned}\]

Au cours du cycle, le système reçoit de la chaleur de la source chaude et reçoit du travail du milieu extérieur ; il cède à la source froide sous forme de chaleur toute l’énergie absorbée. Ce fonctionnement est sans intérêt pratique.

– Dans la région [3] :

\[\begin{aligned} &Q_1+Q_2<0\qquad\Rightarrow\qquad W>0\\ &Q_1<0\quad;\quad Q_2<0\end{aligned}\]

Au cours du cycle, le système reçoit du travail du milieu extérieur et cède cette énergie aux deux sources sous forme de chaleur. Ce fonctionnement ne présente aucun intérêt.

– Dans la région [4] :

\[\begin{aligned} &Q_1+Q_2<0\qquad\Rightarrow\qquad W>0\\ &Q_1<0\quad;\quad Q_2<0\quad;\quad |Q_1|>|Q_2|\end{aligned}\]

Au cours du cycle, le système reçoit du travail du milieu extérieur, emprunte de la chaleur à la source froide et cède toute cette énergie sous forme de chaleur à la source chaude. Le système constitue donc une machine frigorifique.

8. Rendement d’une machine thermique

Une machine thermique dépense du combustible et fournit du travail ; la dépense peut être représentée par la chaleur empruntée à la source chaude (chaudière pour une machine à vapeur, gaz chauds contenus dans le cylindre pour un moteur à explosions).

Le premier principe ne s’opposerait pas à ce que toute l’énergie que représente cette chaleur soit cédée sous forme de travail au milieu extérieur. Nous aurions ainsi une machine transformant intégralement, c’est-à-dire avec un rendement égal à l’unité, la chaleur prise à la source chaude en travail fourni au milieu extérieur.

Le second principe s’y oppose en exigeant qu’une partie de cette énergie soit cédée à la source froide sous forme de chaleur (du moins tant que \(T_1\) et \(T_2\) ne sont ni nulles, ni infinies). Cette énergie peut être considérée comme dépensée en pure perte. Elle aura par exemple été fournie soit à l’atmosphère (gaz d’échappement d’une voiture), soit l’eau de refroidissement d’un condenseur de machine à vapeur.

Le rendement de la transformation \(chaleur~\rightarrow~travail\) est donc nécessairement inférieur à l’unité. \[R=-\frac{W}{Q_1}\qquad;\qquad 0<R<1\]

Ceci parce que le travail fourni au milieu extérieur est \([-W]\).

Remplaçant \([W]\) par \([-(Q_1+Q_2)]\) : \[R=\frac{Q_1+Q_2}{Q_1}=1+\frac{Q_2}{Q_1}\]

Pour toute machine réelle: \[\frac{Q_1}{T_1}+\frac{Q_2}{T_2}<0\qquad\Rightarrow\qquad\frac{Q_2}{Q_1}<-\frac{T_2}{T_1}\]

D’où nous tirons: \[R<\frac{T_1-T_2}{T_1}\]

Pour une machine thermique réversible : \[\frac{Q_2}{Q_1}=-\frac{T_2}{T_1}\quad\Rightarrow\quad R_{rev}=\frac{T_1-T_2}{T_1}\]

Le rendement d’un moteur thermique réel est donc toujours inférieur au rendement d’un moteur réversible fonctionnant entre les mêmes sources de chaleur. Nous avons ainsi démontré comme conséquence du second principe, le Théorème de Carnot, suivant lequel :

• Aucune machine fonctionnant entre deux sources données ne peut avoir un rendement supérieur à celui d’une machine réversible fonctionnant entre les mêmes sources.

et pour son corollaire :

• Toutes les machines réversibles fonctionnant entre deux sources de chaleur données ont même rendement.

9. Rendement d’une machine frigorifique

Nous supposons toujours que la machine fonctionne entre les sources \(C_1\) et \(C_2\). Le point figurant le cycle est maintenant situé dans la région [4] du diagramme de Raveau. Il s’agit d’extraire de la chaleur de la source froide. Le second principe nous apprend que cela ne peut se faire sans la dépense d’un certain travail \(W\) fourni par le milieu extérieur au système (machine frigorifique) au cours du cycle.

Nous pouvons donc définir le rendement de la machine frigorifique comme étant égal au quotient de la chaleur enlevée à la source froide (eau transformée en cubes de glace par exemple) par le travail (électrique en général) fourni par le milieu extérieur. \[R=\frac{Q_2}{W}=\frac{Q_2}{-(Q_1+Q_2)}\]

Dans cette région [4], \(Q_2\) et\( W\) sont positifs. \(R\) est donc positif, mais n’est nullement assujetti à rester inférieur à l’unité, ce qui n’était pas le cas pour les machines thermiques en raison du premier principe.

Écrivons : \[\frac{1}{R}=-1+\Big(\frac{-Q_1}{Q_2}\Big)\]

Pour une machine réelle : \[\frac{Q_1}{T_1}+\frac{Q_2}{T_2}<0\quad\Rightarrow\quad\frac{-Q_1}{Q_2}>\frac{T_1}{T_2}\qquad\text{car :}\quad Q_2>0~~;~~T_1>0\]

On a donc : \[\frac{1}{R}>\frac{T_1}{T_2}-1\qquad\text{soit :}\quad R<\frac{T_2}{T_1-T_2}\]

Si la machine est réversible (par exemple, une machine de Carnot décrivant son cycle en sens inverse du sens moteur), nous obtiendrons : \[R_{rev}=\frac{T2}{T_1-T_2}\]

Le théorème de Carnot et son corollaire s’appliquent donc aussi aux machines frigorifiques dont le rendement est alors défini comme nous venons de l’indiquer.

10. Pompe à chaleur

Dans le paragraphe précédent, nous nous sommes intéressés dans la machine frigorifique à la chaleur prise à la source froide, ce qui semblait naturel. Conservons la même machine frigorifique et intéressons-nous maintenant à la chaleur cédée à la source chaude.

Cette source chaude pourra être par exemple un appartement. L’élément chaud du réfrigérateur se trouve à l’intérieur où il joue le rôle d’un calorifère. L’élément réfrigérant se trouve à l’extérieur et tend à refroidir l’atmosphère de la ville.

Le réfrigérateur, utilisé dans ces conditions, porte le nom de pompe à chaleur. C’est ainsi que fonctionnent les appareils dits à air conditionné.

L’intérêt de ces appareils réside dans le fait qu’ils prennent à l’extérieur la majeure partie de la chaleur qu’ils fournissent à la pièce chauffée. Leur fonctionnement nécessite, il est vrai, la dépense d’énergie mécanique fournie par un moteur électrique, mais la puissance électrique ainsi dépensée est beaucoup mieux utilisée que si on la dissipait par effet Joule dans un radiateur.

Pour calculer le rendement d’une telle pompe à chaleur, nous désignerons par \(T_1\) la température de l’élément chauffant (source chaude) et par \(T_2\) la température de l’élément réfrigérant qui à l’extérieur reçoit constamment de la chaleur de l’air atmosphérique.

Ce qui est dépensé est \(W\), travail électrique absorbé pendant un cycle. Le résultat intéressant est maintenant \((-Q_1)\), chaleur fournie au cours du cycle à la source chaude.

Le rendement s’écrit : \[R=\frac{-Q_1}{W}=\frac{-Q_1}{-(Q_1+Q_2)}=\frac{Q_1}{Q_1+Q_2}\]

On en tire : \[\frac{1}{R}=1+\frac{Q_2}{Q_1}=1+\frac{-Q_2}{-Q_1}\]

Pour une machine réelle : \[\frac{Q_2}{-Q_1}<\frac{T_2}{T_1}\qquad\text{soit :}\quad \frac{1}{R}>1-\frac{T_2}{T_1}\]

En définitive : \[R<R_{rev}=\frac{T_1}{T_1-T_2}\]

Soit par exemple 3 °C la température de l’élément chauffant l’appartement et –5 °C la température à laquelle se maintient, à l’extérieur, l’élément réfrigérant. Supposons réversible le fonctionnement interne. Le rendement est : \[R_{rev}=\frac{303}{303-268}\approx 8,6\]

Cela signifie qu’un kilowatt-heure dépensé pour faire marcher la pompe à chaleur fournit à la pièce chauffée autant de chaleur que celle qui serait dégagée dans un radiateur électrique de 8,6 kWh. On conçoit l’intérêt du dispositif. Cet intérêt disparaîtrait s’il s’agissait de chauffer un four à haute température, \(R\) étant sensiblement égal à 1 pour \(T_1 \gg T_2\).

L’intérêt de l’utilisation d’une pompe à chaleur est d’autant plus grand que l’élévation de température qu’on lui demande de réaliser par rapport à l’extérieur est plus faible, le rendement tendant vers l’infini (en supposant évidemment le fonctionnement réversible) pour \(T_1 = T_2\).

De plus, l’utilisation d’une machine approximativement réversible, permet d’inverser automatiquement son fonctionnement quand en été la température extérieure devient supérieure à la température désirée dans la pièce.

La machine à air conditionné fonctionne indifféremment en pompe à chaleur ou en réfrigérateur, maintenant une température constante dans la pièce moyennant une dépense d’énergie électrique qui croît approximativement avec le carré de la différence de température avec l’extérieur. La chaleur à extraire ou à apporter croît en effet proportionnellement (en gros) à cette différence, et le rendement varie en raison inverse de cette différence (tant qu’elle reste faible).

C’est là un exemple frappant de l’intérêt des transformations réversibles, en regard d’un processus totalement irréversible comme le fonctionnement d’un radiateur électrique.

11. Transformations avec un grand nombre de sources de chaleur

Nous allons considérer tout d’abord un cycle de transformations d’un système quelconque, au cours duquel le système peut recevoir de la chaleur ne plusieurs sources \([C_1,~C_2,~\dots,~C_n]\) aux températures respectives \([T_1,~T_2,~\dots,~T_n]\).

11.1. Cycle réel de transformations

À la fin du cycle, le système a reçu des diverses sources les quantités de chaleur respectives \([Q_1,~Q_2,~\dots,~Q_n]\) et le travail total est \(W\).

Proposons-nous de restituer aux sources \(C_i\) les quantités de chaleur ainsi cédées, de façon à ramener à leur état initial, mais imposons-nous de le faire de façon réversible et en n’empruntant de chaleur qu’à une source unique \(C_0\) à la température \(T_0\).

Une simple mise en contact de sources ne peut convenir, car l’échange de chaleur entre sources à température différente se ferait de façon irréversible, de la plus chaude à la plus froide. Il nous faut donc, pour rendre la chaleur \(Q_i\) à la source \(C_i\) de façon réversible à l’aide de la source \(C_0\), faire fonctionner entre \(C_0\) et \(C_i\) une machine de Carnot. Celle-ci va emprunter la chaleur \((-Q_i)\) à \(C_i\), une certaine chaleur \(Q_0^i\) à \(C_0\), et un certain travail au milieu extérieur : \[W_i=-\{Q_0^i+(-Q_i)\}\]

Nous pouvons supposer tous les travaux extraits d’une seule source d’énergie mécanique (accumulateur par exemple) placée dans le milieu extérieur.

Faisons la même opération pour les \(n\) sources \(C_i\) au moyen de \(n\) machines de Carnot et établissons le bilan total, au point de vue des modifications de l’Univers. Nous aboutissons ainsi à l’inégalité de Clausius : \[\sum\frac{Q_i}{T_i}<0\]

Il en découle une deuxième inégalité dite inégalité de Gouy : \[W+\sum\frac{T_i-T_0}{T_i}~Q_i~>~0\]

11.2. Cycle réversible

On démontre que, pour tout cycle réversible du système:

\[\begin{aligned} &\sum\frac{Q_i}{T_i}=0 &&\text{Clausisus}\\ &W+\sum\frac{T_i-T_0}{T_i}=0 &&\text{Gouy}\end{aligned}\]

Remarque

Dans tous les cas (cycle réel ou réversible), \(T_i\) est la température de la source qui fournit la chaleur \(Q_i\) au système. Dans le second cas (cycle réversible), nous pouvons affirmer en plus que \(T_i\) est aussi la température du système lorsqu’il reçoit la chaleur \(Q_i\) (réversibilité de l’échange de chaleur).

12. Transformation avec une infinité de sources

Nous étendrons immédiatement les résultats du paragraphe précédent au cas d’une infinité de sources de chaleur en remplaçant les sommes par des intégrales.

Si le cycle décrit par le système est un cycle réel, nous désignerons par \(dQ\) la quantité de chaleur infinitésimale fournie au système, pendant son cycle, par la source qui se trouve en ce moment en relation avec lui et dont la température est \(T\).

Nous écrirons :

\[\begin{aligned} &\int_C\frac{dQ}{T}<0\\ &W+\int_C\frac{T-T_0}{T}~dQ>0\end{aligned}\]

Le signe \(\int_C\) indique que l’intégrale se rapporte à un cycle donné des transformations du système.

Il faut bien reconnaître que ces inégalités seront, en général, difficiles à utiliser mathématiquement, la succession des états occupés par le système n’étant pas forcément une succession d’états d’équilibre et \(dQ\) devant donc être déduit à chaque instant des modifications du milieu extérieur.

Passons maintenant au cas où le cycle de transformations décrit par le système est réversible. Les inégalités sont remplacées par des égalités :

\[\begin{aligned} &\int_C\frac{dQ}{T}=0\\ &W+\int_C\frac{T-T_0}{T}~dQ=0\end{aligned}\]

Dans ces intégrales, \(T\) représente non seulement la température de la source qui fournit \(dQ\), mais aussi la température du système lorsqu’il reçoit \(dQ\).

Le cycle étant réversible, \(dQ\) peut à chaque instant être exprimé à partir des coordonnées thermodynamiques du système (et de la variation infinitésimale de certaines d’entre elles). Les égalités sont donc susceptibles d’un maniement mathématique immédiat.

Nous fixerons notre attention sur la première, la seconde s’en déduisant par application du premier principe, et exprimerons le résultat obtenu sous la forme du théorème de Clausius :

• Lorsqu’un système décrit un cycle réversible de transformations, il existe entre les quantités de chaleur \(dQ\) qu’il reçoit aux instants où sa température est \(T\) la relation : \[\int_C\frac{dQ}{T}=0\]