1. Introduction

Jusqu’à présent, nous avons exclu toute possibilité de réaction chimique dans les systèmes chimiques que nous avons étudiés. Cherchons maintenant à éliminer cette restriction.

Considérons par exemple un mélange d’hydrogène et d’oxygène à température ordinaire. Une fois qu’il a atteint l’équilibre mécanique et thermique avec le milieu extérieur, ce mélange semble en équilibre thermodynamique : nous n’avons en effet aucune modification de son état au cours du temps. Introduisons maintenant une quantité très faible de mousse de platine au sein du mélange ; nous observons la combinaison chimique des deux gaz et voyons apparaître la formation d’une certaine quantité d’eau.

Nous en concluons que le mélange oxygène – hydrogène, bien qu’en équilibre mécanique et thermique, n’était pas en équilibre chimique puisque l’introduction d’une quantité infinitésimale du catalyseur que constitue la mousse de platine a suffi à provoquer une modification importante de son état.

Le système oxygène – hydrogène à la température ordinaire est donc dans un état de déséquilibre chimique, mais cette évolution est tellement lente qu’il est impossible de la discerner et que le mélange peut pratiquement se maintenir indéfiniment à la même composition. Nous sommes donc en présence d’un système dont l’évolution vers l’équilibre chimique est tellement lente que la modification qu’elle introduit pendant le temps nécessaire pour que s’établisse l’équilibre mécanique et thermique est complètement négligeable.

Nous pourrons dès lors considérer comme réversibles les transformations au cours desquelles sera constamment maintenu l’équilibre mécanique et thermique. Le mélange gazeux se trouve par conséquent dans une sorte d’équilibre métastable que nous pourrons désigner sous le nom d’équilibre figé. Bien entendu, de nombreuses réactions chimiques seront au contraire beaucoup trop rapides pour qu’il soit possible de négliger l’évolution chimique du système pendant le temps d’établissement de l’équilibre mécanique et thermique.

Cependant, il est souvent possible alors de ralentir considérablement la réaction par l’addition de quantités infinitésimales de corps désignés sous le nom de catalyseurs négatifs ou anticatalyseurs, ou simplement par l’élimination absolue de toutes les impuretés qui peuvent jouer le rôle de catalyseur. Considérons alors un système de corps susceptible de réagir chimiquement. Nous pourrons toujours supposer qu’il est possible de ralentir indéfiniment les réactions chimiques par un artifice convenable ; le système est alors en équilibre figé et l’on peut dès lors le considérer comme formé d’un mélange de corps non réagissants.

Il est alors possible de définir l’entropie et la fonction de Gibbs du système, puis de calculer le potentiel chimique de chacun des constituants lorsque l’équilibre mécanique et l’équilibre thermique sont réalisés. Nous définirons alors l’état du système par les nombres de moles des divers constituants que contiennent les diverses phases ainsi que la pression \(p\) et la température \(T\) communes à l’ensemble du système ; nous calculerons à partir de ces données les diverses fonctions d’état du système (fonction de Gibbs par exemple) de la même façon que pour un ensemble de constituants non réagissants.

Soit \(G_f\) la valeur de cette fonction de Gibbs dans cet équilibre figé. Libérons alors la réaction chimique par l’introduction d’une quantité infime de catalyseur. Le système évolue rapidement vers l’équilibre chimique, c’est-à-dire vers l’état d’équilibre thermodynamique stable.

Soit \(G_e\) la valeur de la fonction de Gibbs lorsque l’équilibre chimique est atteint. Nous avons maintenu la température et la pression constantes pendant l’évolution du système ; nous sommes donc assurés que la fonction de Gibbs a diminué, soit : \[G_e < G_f\]

Cette inégalité nous indique dans quelle direction se produit la réaction chimique. Enfin la recherche de l’équilibre chimique du système se ramène à la recherche de l’équilibre figé pour lequel \(G\) (à \(p\) et \(T\) constants) est minimum. Il est évident en effet que si \(G\) est minimum, aucune modification du système ne peut se produire lors de l’introduction du catalyseur ; le système se trouvait donc déjà en équilibre chimique avant l’introduction du catalyseur.

2. Déplacement de l’équilibre

Nous venons de voir qu’il est possible, par l’emploi d’anticatalyseurs ou quelquefois par la simple suppression d’impuretés jouant le rôle de catalyseurs, d’empêcher la modification chimique d’un système ou tout au moins de les rendre infiniment lentes, ce qui revient au même.

Nous avions déjà rencontré des circonstances analogues dans l’étude des changements de phase ; l’absence de toute poussière permet de comprimer une vapeur à température constante au-dessus de la pression de vapeur saturante ; la poussière joue ici le rôle de catalyseur de condensation pour la vapeur.

Supposons alors qu’un système chimique soit en équilibre thermodynamique (stable) dans certaines conditions de température et de pression. Modifions la pression de \(dp\) et la température de \(dT\). Le système tend à évoluer vers un nouvel état d’équilibre stable. Cette évolution nécessite des modifications internes du système, telles que la modification chimique ou encore le passage des constituants d’une phase à l’autre.

Nous pouvons aussi empêcher par un anticatalyseur la réaction chimique de se produire ; nous pourrons aussi empêcher les passages de matière d’une phase à l’autre par des membranes imperméables et en éliminant toute poussière pouvant jouer le rôle de catalyseur de changement de phase. Nous aurons ainsi empêché les modifications internes et la transformation \((dp,~dT\)) qui se produit alors dans le système est une transformation à modifications internes entravées.

Maintenons alors constantes les nouvelles valeurs de \(T\) et \(p\) et libérons les modifications internes (par exemple en introduisant un catalyseur pour les modifications chimiques ou en donnant au système une secousse violente pour faire cesser les retards aux changements de phase). Le système évolue de façon irréversible, à \(p\) et \(T\) constants, vers l’état d’équilibre stable correspondant à cette température et à cette pression, état qu’il aurait atteint directement à partir de l’état initial si la transformation \((dp,~dT)\) avait été introduite en laissant libres de se produire les modifications internes.

Désignons alors par \(I\) l’état d’équilibre stable initial \((p,~T\)), par \(F\) l’état d’équilibre stable \((p+dp,~T+dT)\) que le système atteint lors de la transformation à modifications internes libres. Désignons enfin par \(F'\) l’état d’équilibre métastable \((p+dp,~T+dT\)) que le système atteint lors de la transformation à modifications internes entravées.

Nous savons que la transformation \(F'\rightarrow F\) se produit naturellement, à la pression constante \(p+dp\) et à la température constante \(T+dT\), lorsqu’on libère les modifications internes. Il en résulte : \[G(F')>G(F)\]

Ceci va nous permettre de définir le sens des modifications internes introduites dans un système chimique par une modification des conditions extérieures telles que la pression et la température, c’est-à-dire les lois du déplacement de l’équilibre dans un système chimique.

2.1. Variation de pression à température constante

Soient \(I(p,~v,~T)\) l’état d’équilibre stable initial, \(F(p+dp,~v+dv,~T+dT)\) l’état d’équilibre stable obtenu par une transformation isotherme à modifications intérieures libres et \(F'(p+dp,~v+dv,~T+dT)\) l’état d’équilibre métastable obtenu par transformation isotherme à modifications intérieures entravées. Nous représentons ces trois états dans le diagramme de Clapeyron (figure ci-contre).

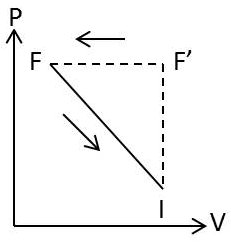Nous pouvons faire décrire au système le cycle monotherme et partiellement irréversible \(IF'\rightarrow FI\). Au cours de ce cycle, le travail reçu est positif ce qui implique que le cycle est nécessairement parcouru dans le sens direct. On en déduit que :

\[\begin{aligned} &dp > 0 \quad\rightarrow\quad V_{F'} > V_F\\ &dp < 0 \quad\rightarrow\quad V_{F'} < V_F\end{aligned}\]

Or, la variation de volume \((V_F-V_{F'})\) est celle qui se trouve entraînée par la modification interne lorsque celle-ci se produit seule, à pression et à température constantes. D’où la loi de Le Châtelier :

L’augmentation, à température constante, de la pression d’un système chimique en équilibre produit dans ce système la modification interne qui, si elle se produisait seule à température et pression constantes, ferait diminuer le volume et qui tend par suite à s’opposer à la modification de pression imposée.

2.2. Variation de température à pression constante

Nous choisissons maintenant le diagramme entropique pour représenter les états du système.

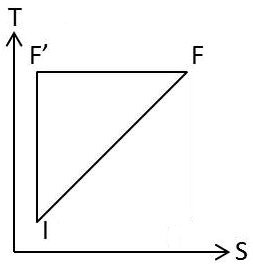\(I(p,~S,~T)\) est l’état d’équilibre stable initial.

\(F(p,~S+dS,~T+dT)\) est l’état d’équilibre stable obtenu par transformations à modifications internes libres

\(F'(p,~S+dS,~T+dT)\) est l’état d’équilibre métastable obtenu par transformation à modifications intérieures entravées.

Nous pouvons écrire \(G_{F'}>G_F\).

Soit: \[{\delta G}_{F'\rightarrow F}=\{\delta(H-TS)\}_{F'\rightarrow F}~<~0\]

Ou encore : \[{\delta G}_{F'\rightarrow F}={\delta(T~S)}_{F'\rightarrow F}\]

Mais on a : \[{\delta(TS)}_{F'\rightarrow F}=\{(T+dT)~\delta S\}_{F'\rightarrow F}\]

Il vient donc : \[{\delta H}_{F'\rightarrow F} < \{(T+dT)~\delta S\}_{F'\rightarrow F}\]

Mais par ailleurs : \[\delta H_{F'-F}=\delta H_{I-F}-\delta H_{I-F'}\]

On a donc : \[\delta H_{F'\rightarrow F}=\int_I^F T~dS-\int_I^{F'}T~dS ~\approxeq~\{(T+dT/2)~\delta S\}_{I\rightarrow F}-\{(T+dT/2)~\delta S\}_{I\rightarrow F'}\]

(On suppose que S varie de façon continue dans les transformations réversibles \(I\rightarrow F\) et \(I\rightarrow F'\)).

Il vient donc : \[\delta H_{F'\rightarrow F}=\{(T+dT/2)~\delta S\}_{F'\rightarrow F}\]

En retranchant de l’inégalité: \[\delta H_{F'\rightarrow F} < \{(T+dT)~\delta S\}_{F'\rightarrow F}\]

Nous obtenons : \[\{T~\delta S\}_{F'\rightarrow F}>0\]

Ou, comme \(T+dT/2\) est évidemment positif : \[\{T~dH\}_{F'\rightarrow F}=\{Q~dT\}_{F'\rightarrow F}>0\]

Si \(dT\) est positif, la chaleur reçue par le système dans la transformation \(F'\rightarrow F\) est positive. Nous en déduisons la loi de Van’t Hoff :

L’élévation, à pression constante, de la température d’un système chimique en équilibre produit dans ce système la modification interne qui, si elle se produisait seule à température et pression constantes, absorberait de la chaleur et qui tend donc à s’opposer à la modification de température imposée.

3. Équilibre chimique en phase unique

Nous considérons une phase formée des constituants \(A_iA'_j\) entre lesquels peut se produire la réaction chimique : \[\sum_i v_i~A_i\quad\rightleftarrows\quad\sum_j v'_j~A'_j\]

Désignons par \(n_i\) et \(n'_j\) les nombres de moles respectifs des divers constituants dans la phase. Si nous choisissons des valeurs quelconques pour les \(n_i\) et \(n'j\), la phase n’est pas en équilibre chimique, mais nous pouvons la considérer instantanément comme en équilibre figé et calculer les potentiels chimiques \(\mu_i\) et \(\mu'_j\) des divers constituants de la même façon que si la réaction chimique n’existait pas. Nous pouvons alors écrire la fonction de Gibbs de la phase sous la forme :

\[G=G(n_i,~n'_j,~T,~p)=\sum_i \mu_i~n_i+\sum_j \mu'_j~n'_j\]

Les \(dn_i\) et \(dn'_j\) ne sont toutefois pas arbitraires. Si la réaction par exemple a progressé vers la droite, il en est résulté un ensemble de \(dn'_j\) positifs et proportionnels aux coefficients \(\mu'_j\) ainsi qu’un ensemble de \(dn_i\) négatifs proportionnels aux coefficients \(\mu_i\), le coefficient de proportionnalité étant le même en valeur absolue. En d’autres termes, toute progression infinitésimale de la réaction entraîne un ensemble de \(dn_i\) et \(dn'_j\) tels que : \[\frac{-dn_1}{v_1}=\dots=\frac{-dn_i}{v_i}=\dots=\frac{dn'_1}{v'_1}=\frac{dn'_1 j}{v'_j}=\dots=d\varepsilon\]

La progression a lieu vers la droite pour \(d\varepsilon\) positif et vers la droite pour \(d\varepsilon\) négatif. La variation la fonction de Gibbs est certainement négative pour toute progression réelle de la réaction. On a donc : \[dG=\sum_i\mu_i~v_i~d\varepsilon+\sum_j\mu'_j~v'_j~d\varepsilon\]

Soit : \[\Big(\sum_i\mu_i~v_i-\sum_j\mu_j~v_j\Big)~d\varepsilon>0\]

Comme \(d\varepsilon>0\), la réaction progresse vers la droite si : \[\sum_i\mu_i~v_i>\sum_j\mu_j~v_j\]

et vers la gauche à contrario.

Il est clair que la condition nécessaire et suffisante pour que la phase soit en équilibre chimique est, \(T\) et \(p\) étant maintenues constantes : \[\sum_i\mu_i~v_i=\sum_j\mu_j~v_j\]

puisque dans ce cas toute modification infinitésimale de l’état de la phase à \(T\) et \(p\) constantes, c’est à dire toute modification infinitésimale de \(\varepsilon\), maintient stationnaire la fonction de Gibbs.

Rappelons que les potentiels chimiques ne dépendent que des concentrations. Nous pouvons dès lors affirmer que :

1. pour tout ensemble de concentrations tel que \(\sum_i\mu_iv_i=\sum_j\mu_jv_j\), la phase est en équilibre chimique ;

2. si les deux sommes sont différentes, la réaction progresse de façon à créer aux dépens des autres les constituants pour lesquels la somme est le plus faible.

4. Équilibre chimique d’un ensemble de gaz parfaits

Nous supposons que les \(A_i\) et les \(A'_j\) sont tous des gaz parfaits. La fonction de Gibbs est alors (voir plus haut) : \[G=R~T~\Big\{\sum_i n_i~[\varphi_i+\ln(p_i)]+\sum_j n'_j~[\varphi'_j+\ln(p'_j)]\Big\}\]

\(p_i\) et \(p'j\) pressions partielles.

Comparant à : \[G=\sum_i \mu_i~n_i+\sum_j \mu'_j~n'_j\]

nous voyons que :

\[\begin{aligned} \mu_i&=R~T~[\varphi_i+\ln(p_i)]\\ \mu'_j&=R~T~[\varphi'_j+\ln(p'_j)]\end{aligned}\]

Soit l’équation d’équilibre, la température et la pression totale étant maintenues constantes : \[G=R~T~\Big\{\sum_i v_i~[\varphi_i+\ln(p_i)]-\sum_j v'_j~[\varphi'_j+\ln(p'_j)]\Big\}=0\]

qui peut s’écrire : \[\ln\frac{p_1^{v1}~p_2^{v2}\dots}{v'_1~v'_2}=\sum_j v'_j~\varphi'_j-\sum_i v_i~\varphi_i=\ln(K)~p'_1~p'_2~\dots\]

Les \(\varphi_i\) et les \(\varphi'_j\) ne dépendant que de la température, il en est de même de la constante \(K\).

Le résultat que nous avons obtenu constitue la loi d’action de masse ou loi de Guldberg et Waage, en vertu de laquelle les pressions partielles des divers gaz réagissant sont liés à l’équilibre par la relation : \[\frac{\Pi_i(p_i^{vi})}{\Pi_j({p'}_j^{v'j})}=K\]

La constante \(K\) ne dépend que de la température. On peut écrire aussi, en introduisant les concentrations moléculaires \(x_i\) et \(x'_j\) et la pression \(P\) du mélange gazeux : \[\frac{\Pi_i x_i^{vi}}{\Pi_i{x'}_j^{vj} }=K~P'\]

avec : \[v=\sum_j v'_j-\sum_i v_i\]

Il est clair que si \(v\) est positif, une élévation de pression fera progresser vers la gauche la réaction (les \(x_i\) allant en croissant). On pouvait le prévoir puisque la réaction s’accompagne dans ce cas, à température constante, d’une augmentation de volume lorsqu’elle s’accomplit vers la droite.

Il suffit alors d’appliquer la loi de Le Châtelier de déplacement à l’équilibre. La constante porte le nom de constante d’équilibre de la réaction.

4.1. Variation de la constante d’équilibre avec la température

Rappelons l’expression : \[\varphi=\frac{H_0^m}{R~T}-\frac{1}{R}\int\frac{\int C_p~dT}{T^2}~dT-\frac{S_0^m}{R}\]

Il en résulte : \[\frac{d\varphi}{dT}=-\frac{H_0^m}{RT^2}-\frac{1}{RT^2}\int C_pdT=-\frac{H^m}{RT^2}\]

\(H^m\) enthalpie d’une mole du gaz parfait à la température \(T\).

Désignons par : \[\Delta H=\sum_j v'_j~H_j^m-\sum_i v_i~H_i^m\]

l’accroissement d’enthalpie lorsqu’on passe des gaz formant le premier membre de la réaction aux gaz formant le second membre.

Nous savons que la chaleur de réaction à pression constante qui correspond à la réaction complète vers la droite : \[\sum_i v_i~A_i\quad\rightarrow\quad\sum_j v'_j~A'_j\]

Soit \(Q_p=-\Delta H\). Dérivons alors : \[\frac{d(\ln K)}{dT}=\sum_j v'_j~\frac{d\varphi'_i}{dT}-\sum_i v_i~\frac{d\varphi_i}{dT}\]

Il en résulte immédiatement que : \[\frac{d(\ln K)}{dT}=-\frac{\Delta H}{R~T^2}+\frac{Q_p}{R~T^2}\]

Équation très importante qui permet par exemple de calculer la chaleur de réaction, lorsque la température trop élevée rend difficiles les mesures calorimétriques, à partir des mesures de concentrations d’équilibre à diverses températures.

On peut par ailleurs calculer directement \(\ln(K)\) sous la forme (équation de Nernst) : \[\ln K=\frac{\Delta H_0}{R~T}-\frac{1}{R} \int\frac{\int C_p~dT}{T^2}~dT-\frac{\Delta S_0}{R}\]

Avec:

\[\begin{aligned} \Delta H_0&=\sum_j v'_j~H_{0j}^m-\sum_i v_i~H_{0i}^m\\ \Delta C_p&=\sum_j v'_j~C_{pj}-\sum_j v_i~C_{pi}\\ \Delta S_0&=\sum_j v'_j~S_{0j}^m-\sum_i v_i~C_{pi}\end{aligned}\]

Les \(C_p\) et leurs variations peuvent être déterminées soit théoriquement, soit par des mesures calorimétriques. L’intégrale du second membre est donc connue.

\(\Delta H_0\) peut de même être déterminé si l’on connaît la chaleur de réaction \(Q_p\) à la température \(T\). On applique la relation : \[-Q_p=\Delta H=\Delta H_0+\int\Delta C_p~dT\]

l’intégrale étant connue.

Il suffit de mesurer \(K\) à une température déterminée pour en tirer \(\Delta S_0\). On connaît alors \(K\) à toutes les températures.

L’intérêt de tout ceci réside surtout dans le fait qu’il suffira de déterminer les valeurs de \(\Delta H_0\) et \(\Delta S_0\) pour quelques réactions importantes pour pouvoir en déduire par combinaisons les valeurs de \(\Delta H_0\) et \(\Delta S_0\) pour un grand nombre d’autres réactions.

Par exemple, on trouve :

\[\begin{aligned} &H_2+\frac{1}{2}O_2\quad\leftrightarrow\quad H_2O\\ &\Delta H_0=-2,39\times 10^5~J~mole^{-1}\quad;\quad\Delta S_0=-14,6~J~mole^{-1}~K^{-1}\\ &CO+\frac{1}{2}O_2\quad\leftrightarrow\quad CO_2\\ &\Delta H_0=-2,79\times 10^5~J~mole^{-1}\quad;\quad\Delta S_0=-18,6~J~mole^{-1}~K^{-1}\end{aligned}\]

On en tire par différence pour la réaction :

\[\begin{aligned} &CO+H_2O\quad\leftrightarrow\quad CO_2+H_2\\ &\Delta H_0=-4,0\times 10^4~J~mole^{-1}\quad;\quad\Delta S_0=-4,0~J~mole^{-1}~K^{-1}\end{aligned}\]

d’où la constante d’équilibre de cette dernière réaction à toute température.

5. Équilibre chimique en phases multiples

Nous supposons maintenant que le système des corps réagissant \(A_i\) et \(A_j\) comprend plusieurs phases. Il est clair que l’équilibre du système, la température et la pression étant imposées, exige :

• que le potentiel chimique de chacun des constituants soit le même dans toutes les phases. Soit \(c=(\varphi-1)\) équations ;

• qu’entre les potentiels chimiques existe la relation d’équilibre : \[\sum_i \mu_i~v_i=\sum_j\mu'_j~v'_j\]

5.1. Règle des phases en présence de réactions chimiques

Nous venons de voir que la présence d’une réaction chimique abaisse d’une unité la variance du système puisqu’une équation supplémentaire vient lier les paramètres chimiques. On trouverait de même que la présence de réactions chimiques indépendantes (c’est-à-dire telles qu’aucune d’entre elles ne puisse se déduire d’une combinaison des autres) abaisse de \(r\) unités la variance du système.

Il peut arriver d’ailleurs que d’autres équations restrictives viennent encore abaisser la variance. Ce sera le cas si le système est constitué de telle sorte qu’un rapport fixe se trouve imposé entre les concentrations de certains des constituants. Par exemple, considérons la réaction d’équilibre : \[NH_4HS\quad\leftrightarrow\quad NH_3+H_2S\]

Elle contient deux phases : une phase solide \(NH_4HS\) et une phase gazeuse \(NH_3+H_2S\).

Supposons que le système soit constitué en mettant en présence des quantités arbitraires des trois constituants \(NH_4HS~;~NH_3~;~H_2S\). Sa variance est alors : \[V=c+2-\varphi-1=2\]

À chaque température et à chaque pression correspond une composition de la phase gazeuse qui assure l’équilibre. Si nous constituons le système en introduisant au départ du sulfure d’ammonium dans une enceinte vidée, nous imposons alors aux concentrations de l’ammoniac et de l’hydrogène sulfuré d’être constamment égales dans la phase gazeuse soit une condition supplémentaire et abaissement de la variance d’une unité. Elle devient alors égale à 1 et à chaque température correspond une pression d’équilibre bien déterminé.

Désignant alors par \(r\) le nombre de réactions indépendantes, par \(s\) le nombre d’équations restrictives, nous obtenons en définitive la variance : \[V=(c-r-s)+2-\varphi=c'+2-\varphi\]

en désignant par \(c'\) le nombre \((c-r-s)\) de constituants indépendants du système.