1. Liquéfaction des gaz

Un gaz qui, à la température ambiante, est au-dessous de sa température critique se liquéfie par simple compression à la température ordinaire. On peut alors, soit le conserver à l’état liquide à la température ordinaire et à haute pression (par exemple, l’ammoniac \(NH_3\) est liquide à 20 °C sous la pression de 9 atmosphères), soit le verser dans un vase de Dewar.

Le retour à la pression atmosphérique entraîne une ébullition violente, l’évaporation d’une partie du liquide amenant le reste à une température assez basse pour que l’équilibre se maintienne à la pression atmosphérique. On obtiendra donc par exemple de l’ammoniac liquide à la pression atmosphérique par compression isotherme à 20 °C de 1 à 10 atmosphères, suivie d’une détente adiabatique (approximativement) de 10 à 1 atmosphère.

Un gaz dont la température critique \(T_c\) est inférieure à la température ambiante exige un refroidissement préalable au-dessous de \(T_c\) pour pouvoir être liquéfié par compression. Ce refroidissement pourra être obtenu au moyen d’ammoniac liquide ; on conçoit donc la possibilité de liquéfier la plupart des gaz au moyen d’étages de refroidissement :

• Montage à chlorure de méthyle : Le chlorure de méthyle est liquéfié à la température ordinaire par compression à 5 atmosphères. On l’évapore rapidement sous une pression de 6 cm de mercure, il atteint la température de –70 °C.

• Montage à éthylène : L’éthylène, maintenu à –150 °C se liquéfie à 5 atmosphères. On l’évapore ensuite rapidement sous une pression de 1.5 cm de mercure. Sa température descend à –150 °C.

• Montage à oxygène : L’oxygène, maintenu à –150 °C se liquéfie à 10 atmosphères. Ramené à la pression atmosphérique, il se fixe à –185 °C. En l’évaporant rapidement sous pression de 6 cm de mercure, on atteint –200 °C, température assez basse pour liquéfier l’azote.

1.1. Hydrogène et hélium

La température –200 °C est encore bien supérieure à la température critique de l’hydrogène (33 K ou –240 °C) ou à fortiori de l’hélium (\(T_c\) = 5 K). On se trouve donc contraint pour liquéfier ces deux derniers gaz à faire appel à une détente.

Le plus simple consiste à utiliser la détente Joule-Kelvin à travers un étranglement : l’appareil ne comporte aucune partie rotative difficile à lubrifier à basse température.

Nous savons cependant qu’un gaz ne peut être liquéfié par détente Joule-Kelvin que si son état initial est déjà très voisin des conditions critiques. On y arrive en refroidissant le gaz qui va subir la détente au moyen du gaz qui l’a déjà subie, dans un échangeur de température.

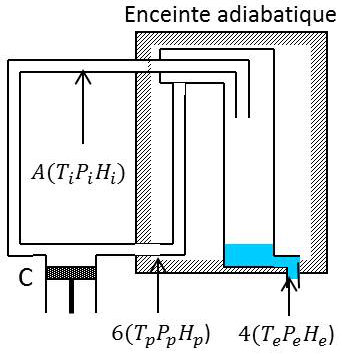Le gaz, comprimé par le compresseur C et refroidi dans le serpentin S, entre en A dans l’échangeur, à la température \(T_i\) et à la pression \(p\) ; l’enthalpie d’un gramme de gaz dans ces conditions est \(H_i\). Il subit dans l’étranglement E une détente Joule-Kelvin, qui abaisse sa température si les conditions \(T_i,~P_i\) sont convenables.

Remontant dans l’échangeur, il refroidit alors le gaz qui va subir la détente ; la température atteinte lors de la détente devient plus basse, et ainsi de suite jusqu’à ce qu’un régime permanent soit atteint ou la détente entraîne une condensation partielle.

Supposons atteint ce régime permanent. Soient \(T_f\) (voisin de \(T_i\) si l’échangeur est efficace), \(P_f\) et \(H_f\) la température, la pression et l’enthalpie spécifique du gaz lorsqu’il quitte l’échangeur pour retourner au compresseur. Soient enfin \(T_1\), \(P_1\) et \(H_1\) la température, la pression et l’enthalpie spécifique du liquide obtenu.

Pour chaque gramme de gaz entrant dans l’échangeur dans les conditions \(T_i,~P_i,~H_i\), la détente produit \(x\) grammes de liquide (conditions \(T_1,~P_1,~H_1\)) et \((1-x)\) grammes de gaz qui sortent de l’échangeur dans les conditions \(T_f,~P_f,~H_f\)).

L’échangeur étant isolé thermiquement, tous les phénomènes qui se produisent dans l’échangeur et l’étranglement sont des détentes sans échange de chaleur ni travail avec le milieu extérieur autres que le travail \(P_i~V_i\) reçu à l’entrée et le travail \(P_f~V_f\) fourni à la sortie.

On peut écrire : \[H_i=x~H_1+(1-x)~H_f\quad\Rightarrow\quad x=\frac{H_f-H_i}{H_1-H_f}\]

La pression \(P_1\) et par suite la température \(T_1\) du liquide sont imposées, donc \(H_1\) est imposée. De même, \(T_i\) est imposée par le serpentin de refroidissement préalable et par suite \(T_f\) qui est voisine de \(T_i\). La pression \(P_f\) étant imposée par la perte de charge dans la canalisation de retour de l’échangeur, \(H_f\) est imposée.

Seule la pression \(P_i\) peut être judicieusement choisie pour rendre le rendement en liquide optimum. Il faut pour cela que \(H_1\) soit minimum, comme le montre l’expression de \(x\) où seule \(H_i\) peut varier, \(T_i\) étant imposée ; \(H_i\) est minimum lorsque : \[\Big(\frac{\partial H_i}{\partial P}\Big)_{T=T_i}=0\]

Mais on a : \[\Big(\frac{\partial H}{\partial P}\Big)_T=-\Big(\frac{\partial H}{\partial P}\Big)_P~\Big(\frac{\partial H}{\partial P}\Big)_H=-c_p~\mu\]

Pour que le rendement en liquide soit optimum, il faut donc que \(\mu=0\) pour \(T=T_i\), c’est-à-dire que les conditions initiales se trouvent sur la courbe d’inversion par effet Joule. On peut ainsi obtenir l’hydrogène bouillant à 20 K à la pression atmosphérique. Évaporé à pression réduite sous 4 cm de mercure, l’hydrogène liquide atteint son point triple à 14 K et se solidifie partiellement.

De la même façon, l’hélium liquide refroidi préalablement dans le serpentin S par de l’hydrogène bouillant sous pression réduite et entrant alors dans l’échangeur de températures, y atteint en régime permanent une température assez basse pour être liquéfié par la détente de Joule-Kelvin. On peut le recueillir liquide à la pression atmosphérique, sa température est environ 4 K environ. En évaporant l’hélium sous pression réduite à 3 cm de mercure, on l’amène à 1,6 K. Au moyen de pompes très puissantes, on peut l’évaporer assez vite pour que sa pression descende à \(3~\mu m\) de mercure : sa température est alors 0,71 K.

On ne peut aller plus bas : la présence du film de Rollin entraîne l’hélium liquide vers le tube de pompage où il se vaporise (région plus chaude) sans extraire de calories à la masse d’hélium liquide du fond du récipient. On sait que de toute façon l’hélium ne peut être solidifié que si sa pression est supérieure à 25 atmosphères. On solidifie donc l’hélium en l’amenant à une pression supérieure à 25 atmosphères au voisinage de 1 K au moyen d’hélium bouillant sous pression réduite.

2. Basses températures par démagnétisation adiabatique

Nous venons de voir qu’on ne peut descendre au-dessous de 0,7 K par évaporation rapide de l’hélium liquide. Nous allons maintenant étudier le procédé imaginé indépendamment par Debye et Giauque en 1926 et expérimenté par Giauque, grâce auquel des températures extrêmement basses peuvent être atteintes par démagnétisation adiabatique d’un solide paramagnétique.

2.1. Principe de la méthode

Soit un solide paramagnétique en forme de tore et entouré par un enroulement qui permet d’établir en son sein une excitation magnétique \(H\). Nous considérerons le solide comme de volume invariable. Il constitue donc un système thermodynamique qui ne peut recevoir de travail que de l’excitation magnétique (c’est-à-dire du courant magnétisant).

Nous définirons alors le solide par sa température \(T\) et son excitation magnétique \(H\). Sa susceptibilité magnétique dépendant de \(T\), l’intensité d’aimantation commune à chacun des éléments de volume du solide est fonction de \(H\) et de \(T\). Considérons alors un volume de solide égal à l’unité.

Pour toute modification de l’intensité d’aimantation, ce volume reçoit un travail du milieu extérieur, d’une façon que nous pouvons considérer comme réversible : \[dT=H~d\mathcal{J}\]

Toute variation \(dT,~dH\) de l’état du solide entraîne donc pour l’unité de volume une variation de sa fonction de Helmoltz : \[dF=h~d\mathcal{J}-S~dT\]

Introduisant la fonction de Gibbs :

\[\begin{aligned} G&=-\mathcal{J}~H-S~T\\ dG&=-\mathcal{J}~dH-S~dT\end{aligned}\]

nous en tirons la relation qui exprime que \(dG\) est une différentielle totale : \[\Big(\frac{\partial S}{\partial H}\Big)_T=\Big(\frac{\partial\mathcal{J}}{\partial T}\Big)_H\]

Écrivons alors l’expression de la chaleur absorbée par le solide dans la transformation \([dH,~dT]\) : \[dQ=T~dS=T~\Big(\frac{\partial S}{\partial T}\Big)_H~dT+T~\Big(\frac{\partial S}{\partial H}\Big)_T~dT\]

Avec : \[\Big(\frac{\partial S}{\partial T}\Big)_H=\frac{C_H}{T}\]

\(C_H\) : capacité calorifique à excitation constante par unité de volume

et avec : \[\Big(\frac{\partial S}{\partial T}\Big)_T=\Big(\frac{\partial\mathcal{J}}{\partial T}\Big)_H\]

nous obtenons en définitive : \[dQ=C_H~dT+T~\Big(\frac{\partial\mathcal{J}}{\partial T}\Big)_H~dH\]

Or, on a : \[\Big(\frac{\partial\mathcal{J}}{\partial T}\Big)_H <~0\]

La loi de Curie par exemple exige que la susceptibilité magnétique décroisse lorsque \(T\) augmente. Il en résulte que l’intensité d’aimantation \(\mathcal{J}\) décroît lorsque \(T\) augmente à \(H\) constant.

Nous voyons alors qu’une augmentation de l’excitation \(H\) à \(T = cte\) entraîne un dégagement de chaleur par la substance dont l’entropie diminue (ceci résulte du fait que la substance est plus ordonnée à forte excitation qu’à faible excitation).

Partons alors d’une forte excitation et supprimons cette excitation en isolant thermiquement la substance paramagnétique (désaimantation adiabatique). Celle-ci va se refroidir : toute modification \(dH\) adiabatique entraînant, puisque \(dQ = 0\), une variation de température (négative lorsque \(dH\) est négatif) : \[dT=-\frac{T}{C_H}~\Big(\frac{\partial\mathcal{J}}{\partial T}\Big)_H~dH\]

Pour atteindre de très basses températures, il faudra donc :

1. porter la substance à très haute excitation magnétique \(H_i\) en maintenant sa température à une valeur très basse au moyen d’hélium bouillant à basse pression \((\approx 1~K)\) ;

2. isoler thermiquement la substance et ramener à une valeur très faible \(H_f\) l’excitation \((H_f\approx 0)\).

Résultats

La température obtenue en fin de démagnétisation dépend de la substance utilisée ; on peut la déterminer par une mesure magnétique de la susceptibilité finale (voir plus loin). En 1933, Giauque avait ainsi atteint une température finale de 0,25 K au moyen de sulfate de gadolinium démagnétisé à partir des conditions initiales : \(T_i=1,5~K~;~H_i\approx 640~000~A/m\).

On tend maintenant à utiliser comme substance paramagnétique des aluns (alun de fer et d’ammonium, alun de chrome). De Klerk et ses collaborateurs ont pu ainsi atteindre en 1951 la température extrême \(T_f\) de 0,0014 K en partant d’une excitation initiale de quelques 106 A/m.

2.2. Détermination de la température \(T_f\)

La susceptibilité magnétique \(J/H\) en fin d’opération est mesurée au moyen d’un galvanomètre balistique. Si la substance suivait la loi de Curie \(\chi T=C=Cte\) jusqu’au zéro absolu, on en tirerait immédiatement la température thermodynamique \(T_f\).

En fait, la quantité \(C / \chi_f=\theta_f \) diffère notablement de \(T_f\), la loi de Curie devenant grossièrement fausse au voisinage du zéro absolu. On mesure donc en fait une quantité \(\theta_f\) que nous pourrions désigner sous le nom de température magnétique et dont nous allons déduire la température thermodynamique.

Désignons dans ce but par \(i\) l’état initial de la substance, par \(k\) l’état atteint par aimantation isotherme \([T_i~,H_i]\) et par \(f\) l’état final après démagnétisation adiabatique \([T_f,~H=0]\). Nous pouvons écrire : \[S_f=S_k\qquad\text{et par suite :}\quad S_f-S_i=S_k-S_i\]

Or : \[S_k-S_i=\frac{Q_i}{T_i}\]

\(Q_i\) étant la chaleur (négative) absorbée pendant l’aimantation isotherme que nous pouvons déterminer par voie calorimétrique.

Maintenant \(Ti = cte\), nous pouvons faire varier \(H_i\) et mesurer dans chaque cas \(Q_i\), soit en définitive \(S_f – S_i\) qui est égal à \(S_k – S_i\). Portant en ordonnée \(S_f – S_i\) en fonction de la température magnétique en fin d’opération \(T_f\), nous obtenons un graphique dont la pente en chaque point nous donne la valeur de : \[\frac{d(S_f-S_i)}{d\theta_f}=\Big(\frac{\partial S}{\partial\theta_f}\Big)_{H=0}\qquad\text{puisque}\quad S_i=cte\]

Considérons maintenant la substance dans l’état \(f\) et, en maintenant \(H = 0\), faisons-lui absorber une quantité d’énergie connue \(dU\) (par exemple par absorption de rayons \(\gamma\) ), mesurons l’augmentation \(d\theta_f\) de température magnétique qui en résulte. Nous pouvons écrire : \[dU=dQ+H~d\mathcal{J}\qquad\text{soit :}\quad dU=dQ\quad\text{pour}\quad H=0\]

La quantité \[\frac{dQ}{d\theta_f}=\Big(\frac{\partial U}{\partial\theta_f}\Big)_{H=0}\]

est donc connue, d’où \(T_f\) au moyen de la relation : \[T_f=\Big(\frac{\partial S}{\partial U}\Big)_{H=0}=\frac{(\partial S/\partial\theta_f)_{H=0}}{(\partial U/\partial\theta_f)_{H=0}}\]

Aux très basses températures, l’écart entre \(T_f\) et \(\theta_f\) peut être considérable ; par exemple, dans le cas de l’alun de chrome et de potassium, on constate que :

• pour \(\theta\) = 0,064 K, \(T\) = 0,035 K ;

• pour \(\theta\) = 0,033 K, \(T\) = 0,0039 K.

3. Capacité calorifique des sels paramagnétiques à TBT

Nous avons fait intervenir dans le paragraphe précédent la quantité \((\partial U/\partial\theta_f)_{H=0}\). Elle est égale à la capacité calorifique à excitation nulle de la substance, mesurées dans l’échelle des températures magnétiques. Il est aisé d’en déduire la capacité calorifique à excitation nulle : \[C_{H=0}=\Big(\frac{\partial U}{\partial T}\Big)_{H=0}\]

Cette capacité calorifique tend vers zéro avec \(T\) comme c’est la règle générale pour tous les solides, mais sa variation avec \(T\) n’est pas du tout la même que celle qu’on observe pour les solides non paramagnétiques où \(C\) tend vers zéro comme \(T^3\) (loi de Debye). La loi usuelle en \(T^3\) résulte en effet du fait que la forme d’énergie qui varie avec \(T\) se réduit pour les solides usuels à l’énergie de vibration des atomes du réseau.

Dans le cas d’une molécule paramagnétique telle que l’alun de chrome, l’atome de chrome responsable du paramagnétisme est placé dans le champ électrostatique de ses voisins et se trouve ainsi susceptible d’occuper deux niveaux d’énergie distincts \([E_0,~E_0+\varepsilon]\).

La population respective de ces deux niveaux dépend de la température ; en termes plus précis, considérons une mole de la substance contenant \(N\) molécules \(\{CrX(SO_4)_2~,~12~H_2O\}\) et par suite \(N\) atomes de chrome. Les nombres \(n_1\) et \(n_2\) d’atomes de chrome occupant respectivement les énergies \(\{E_0,~E_0+\varepsilon\) sont dans le rapport : \[\frac{n_1}{n_2}=\exp(-\varepsilon/k~T)\]

Nous en tirons : \[\frac{n_1}{N}=\frac{\exp(-\varepsilon/k~T)}{1+\exp(-\varepsilon/k~T)}\]

Soit un nombre d’atomes Cr par mole, d’énergie \((E_0+\varepsilon)\)  : \[n_1=N~\frac{\exp(-\varepsilon/k~T)}{1+\exp(-\varepsilon/k~T)}\]

Élevons la température de \(dT\). Le nombre d’atomes d’énergie \((E_0+\varepsilon)\) varie, d’où une variation de l’énergie molaire : \[(dU)_{H=0}=C_H~dT=\varepsilon~dn1=\varepsilon~\frac{d}{dT}~\Big\{N~\frac{\exp(-\varepsilon/k~T)}{1+\exp(-\varepsilon/k~T)}\Big\}~dT\]

On en tire : \[C_H~dT=\varepsilon~dn1=N~\varepsilon~\frac{d}{dT}~\Big\{\frac{\exp(-\varepsilon/k~T)}{1+\exp(-\varepsilon/k~T)}\Big\}~dT=\frac{N~\varepsilon^2}{k~T^2}~\Big\{\frac{\exp(-\varepsilon/k~T)}{1+\exp(-\varepsilon/k~T)}\Big\}\]

Et enfin, avec \(N~k=R\) : \[C_H=R\frac{\varepsilon^2}{k~T^2}~\frac{\exp(-\varepsilon/k~T)}{\{1+\exp(-\varepsilon/k~T)\}^2}\]

\(C_H\) part de zéro pour \(T = 0\), croît rapidement jusqu’à un maximum, puis décroît comme \(1/T^2\). C’est bien ce que montre l’expérience. Aux très basses températures, la capacité calorifique \(C_H\) est beaucoup plus forte que celle d’une substance ordinaire obéissant à la loi de Debye et pour laquelle seules interviennent les vibrations du réseau pour modifier l’énergie interne.

4. Supraconductivité

La plupart des métaux voient leur résistivité décroître lorsque la température s’abaisse et tendre vers une limite non nulle (résistivité résiduelle) pour \(T\rightarrow 0\). Pour certains métaux cependant, si l’on continue à abaisser la température alors que la résistivité résiduelle semble atteinte, on voit brusquement la résistivité tomber à 0.

C’est le phénomène de supraconductivité qui apparaît aussi bien pour certains alliages que pour certains métaux purs. Dans le cas des métaux purs, la chute de résistivité est très brutale : la résistivité tombe à zéro sur un intervalle de température de l’ordre du centième de degré, la transition ayant lieu à une température bien définie. Pour l’aluminium, la température de transition est 1,175 K, pour le zinc 0,946 K.

Ces températures de transition sont celles que l’on observe lorsque le métal n’est soumis à aucune excitation magnétique. L’application d’une forte excitation magnétique a pour résultat de supprimer la supraconductivité. Plus précisément, si l’excitation \(H\) est progressivement établie, on observe la disparition brutale de la supraconductivité lorsque \(H\) atteint un certain seuil \(H_S\).

Si \(T_0\) est la température de transition à excitation nulle, l’excitation seuil faisant disparaître la supraconductivité est donnée par une relation de la forme : \[H_S=H_0~\Big(1-\frac{T^2}{T_0^2}\Big)\]

L’excitation nécessaire pour faire disparaître la supraconductivité est donc d’autant plus forte que la température est plus basse, elle est maximum et égale à \(H_0\) pour \(T = 0\).

4.1. Propriétés paramagnétiques des supraconducteurs

Soit un métal pur dans l’état supraconducteur. Élevons progressivement son excitation magnétique (le métal est par exemple pris sous forme d’une longue aiguille parallèle à la direction de l’excitation, direction qui est alors la même à l’intérieur et à l’extérieur du métal).

Pour chaque valeur de \(H\), mesurons l’induction dans le métal. Nous observons que celle-ci reste nulle tant que \(H < H_S\), c’est-à-dire tant que le métal reste supraconducteur.

La relation \[B=\mu_0~(H+\mathcal{J})\]

indique dès lors que \(\mathcal{J}=H\) tant que le métal est supraconducteur.

Quand \(H\) traverse la valeur \(H_S\), la supraconductivité disparaît et \(B\) devient brusquement égal à \(H\) \((\mathcal{J}=0)\). Il se produit donc un changement d’état lorsque la supraconductivité disparaît.

Désignons par l’indice \(s\) les quantités relatives à l’état supraconducteur et par l’indice \(n\) les quantités relatives à l’état normal. Nous pouvons introduire la fonction de Gibbs généralisée :

\[\begin{aligned} G'&=U-T~S-H~\mathcal{J}\\ \text{de différentielle :}\quad dG'&=-S~dT-\mathcal{J}~dH\end{aligned}\]

On écrira, \(H_S\) étant l’excitation seuil à la température \(T\), que dans les conditions \([T,~H_S]\) de la transition : \[G'_S=G'_n\]

À la température \(T + dT\), l’excitation seuil est \(H_S + dH_S\). Nous écrirons alors :

\[\begin{aligned} dG'_S&=dG'_n\\ \text{soit :}\quad -S_SdT-\mathcal{J}_S~dH_S&=-S_n~dT-\mathcal{J}_n~dH_S\end{aligned}\]

D’où : \[-\frac{dH_S}{dT}=\frac{S_n-S_S}{\mathcal{J}_n-\mathcal{J}_S}\]

Comme :

\[\begin{aligned} \mathcal{J}_n-\mathcal{J}_S&=0-(-H_S)\\ \text{et :}\qquad S_n-S_S&=\frac{L}{T}\end{aligned}\]

\(L\) désignant la chaleur latente de transformation,

on en tire donc : \[L=-T~H_S~\frac{dH_S}{dT}\]

Ceci montre que la transition de l’état normal à l’état supraconducteur (chaleur latente \(-L\)) est une transition de première espèce (\(-L\neq 0\)) en présence d’une excitation magnétique, mais devient une transition de seconde espèce en l’absence d’excitation magnétique \((-L = 0)\).

4.2. Conductibilité thermique des supraconducteurs

La conductibilité thermique d’un métal ordinaire croît tout d’abord lorsque la température s’abaisse, puis passe par un maximum et décroît linéairement avec \(T\) aux très basses températures. Si toutefois le métal devient supraconducteur, la conductivité thermique décroît rapidement et tend vers zéro comme \(T^3\).

Ce phénomène très curieux permet par exemple de transformer instantanément un métal supraconducteur, qui constitue un mauvais conducteur thermique, en un bon conducteur thermique en lui appliquant une excitation magnétique qui fait disparaître la supraconductivité.

5. Essai théorique pour obtenir un zéro absolu

Nous avons vu qu’il est possible d’atteindre par aimantation isotherme suivie d’une démagnétisation adiabatique d’un sel paramagnétique, une température de l’ordre de 0,001 K. Rien ne nous interdit alors d’imaginer que l’on prépare ainsi une grande quantité de substance paramagnétique à 0,001 K, puisque l’on utilise cette masse comme source de chaleur pour maintenir constante pendant son aimantation la température d’une petite quantité supplémentaire de la même substance (la masse principale restant évidemment dans une excitation nulle).

Nous obtenons alors un état de température 0,001 K et d’aimantation élevée, à partir duquel une désaimantation adiabatique va nous permettre d’atteindre une température finale basse, et ainsi de suite.

Pour permettre le passage rapide de l’aimantation isotherme (bon contact thermique entre la substance et la masse principale) on peut par exemple mettre la substance en contact thermique avec la masse principale avec un métal supraconducteur qui, tant que l’aimantation progresse, perd sa supraconductivité et constitue un bon conducteur thermique et qui, lorsqu’on supprime l’excitation pour désaimanter la substance, redevient supraconducteur, donc isolant thermique.

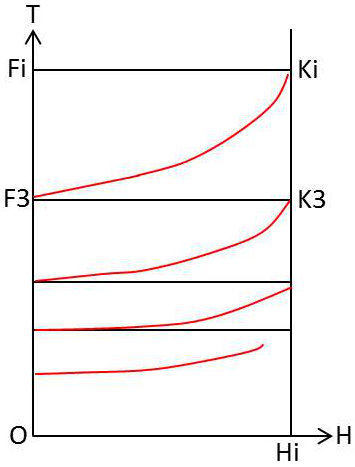Rien ne nous empêche alors d’imaginer une cascade de tels processus où la température finale s’abaisse constamment. La question qui se pose est alors la suivante : est-il possible d’atteindre ainsi le zéro absolu ?

On remarque alors que chaque démagnétisation réduit à peu près dans le même rapport la température, de sorte qu’il faudra un nombre infini d’opérations pour atteindre le zéro absolu. La suite des états occupés par la substance est représentée dans un diagramme \([T,~H]\).

Le procédé de démagnétisation en cascade ne permettrait donc d’atteindre le zéro absolu que par un nombre infini d’opérations. Étudiant tous les procédés possibles (évaporation adiabatique d’un liquide par exemple), on aboutirait à la même conclusion. Nous poserons dès lors le principe suivant :

Aucun processus, même théorique, ne permet d’amener à zéro la température thermodynamique d’un système par un nombre fini d’opérations.

6. Troisième principe de la thermodynamique

Le principe que nous venons d’énoncer s’identifie au troisième principe de la thermodynamique tel qu’il a été énoncé par Nernst :

La variation d’entropie associée à toute transformation isotherme et réversible en milieu condensé tend vers zéro lorsque la température de transformation tend vers zéro.

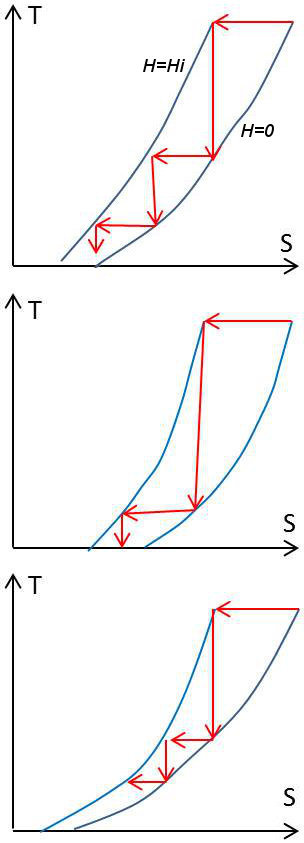Vérifions-le dans le cas de notre expérience de démagnétisation en cascade. Représentons dans ce but les états successifs occupés par la substance paramagnétique dans le diagramme entropique (figures ci-contre).

Traçons sur ce diagramme les deux courbes \([H = 0]\) et \([H = H_i\)], c’est-à-dire \([S = f(T,~H_i)]\) et \([S = f(T,~0)]\).

Si ces deux courbes venaient couper l’axe \(T = 0\) en deux point différents (figure 1 et figure 2), il serait possible, comme le montrent les figures d’atteindre la température \(T = 0\) au moyen d’un nombre fini d’opérations (ceci même dans le cas de la figure 2 qui correspond à une substance hypothétique qui s’échaufferait par démagnétisation adiabatique).

La disposition de figure est donc celle de la figure 3, soit : \(S(0,~H_i) = S(0,~0)\) quel que soit \(H_i\).

La démonstration peut être généralisée de façon à établir l’identité complète du principe d’inaccessibilité du zéro absolu et du troisième principe sous la forme de Nernst.

Remarquons que l’énoncé de Nernst se restreint aux transformations entre états condensés de la matière. Il n’est utilisable en effet que si l’entropie reste finie au zéro absolu. Appliquons alors l’entropie sous l’une ou l’autre des formes :

\[\begin{aligned} S(T,~V)&=\int_0^T\frac{C_V}{T}~dT+f(V)\\ S(T,~P)&=\int_0^T\frac{C_P}{T}~dT+g(P)\end{aligned}\]

Ceci exige que \(C_V/T\) et \(C_P/T\) restent finis au zéro absolu, c’est-à-dire que \(C_V\) et \(C_P\) tendent vers zéro quand \(T\rightarrow 0\). C’est bien ce que l’on observe pour toutes les substances condensées.

Les gaz parfaits semblent cependant échapper à cette règle, \(C_V\) et \(C_P\) tendant vers une limite différente de zéro pour \(T\rightarrow 0\) d’après la statistique classique de Maxwell-Boltzmann. Il est toutefois difficile d’admettre qu’un corps puisse subsister à l’état parfait à une pression non nulle et au zéro absolu.

Signalons d’ailleurs que les statistiques quantiques modifient à très basse température la loi des gaz parfaits de telle sorte que l’entropie tende vers une limite finie pour \(T\rightarrow 0\), cette limite étant nulle si l’on ne tient pas compte de la structure interne des noyaux atomiques.

Nous n’insisterons pas davantage sur ce sujet, et retiendrons simplement qu’il faut se garder de chercher à appliquer le principe de Nernst en extrapolant sans précaution jusqu’au zéro absolu les propriétés de la matière à basse température.

Considérons à titre d’exemple une application classique du principe de Nernst à la transformation allotropique étain blanc – étain gris, qui se produit à 19 °C (292 K) à la pression atmosphérique. Écrivant qu’à l’équilibre les fonctions de Gibbs relatives à l’unité de masse sont égales, nous aurons dans cette transformation : \[\Delta(H-T~S)=0\qquad\text{soit~:}\quad T~\Delta S=\Delta H\]

\(\Delta H\), chaleur de transformation, est trouvée égale à –2260 joules ; on en tire \(\Delta S\) à 19 °C, ce qui conduit, connaissant les chaleurs spécifiques des deux variétés allotropiques, à : \[\Delta S_{25~^oC}=-7,82~J/K\]

Or, le principe de Nernst exige que \(\Delta S_{0~K}=0\). Connaissant les chaleurs spécifiques à pression constante des deux variétés allotropiques et leur variation avec \(T\), on en tire : \[\Delta S_{25~^oC}=-7,11~J/K~\pm~10~\%\]

L’accord est donc satisfaisant. De nombreuses réactions chimiques ont ainsi permis de vérifier le principe de Nernst.