1. Introduction
Il existe quatre types de modulations d’amplitude courantes :
-
la modulation DBSP (double bande sans porteuse) utilisée pour constituer le multiplex stéréophonique ;
-
la modulation DBAP (double bande avec porteuse), dite MA (modulation d’amplitude), très répandue en radiodiffusion ondes courtes, moyennes ou longues ;
-
la modulation BLR (bande latérale résiduelle) utilisée en téléphonie (multiplex) et en radiocommunications militaires ;
-
la modulation BLU (bande latérale unique) employée pour la transmission du signal vidéo en télévision.
2. Modulation sans porteuse
Prenant l’exemple de la modulation d’amplitude, la notion première de modulation peut être associée à celle du battement. Soit deux mouvements sinusoïdaux : \[s_0(t)=a_0~\cos(\omega_0~t)\quad;\quad s_1(t)=a_1~\cos(\omega_1~t)\]
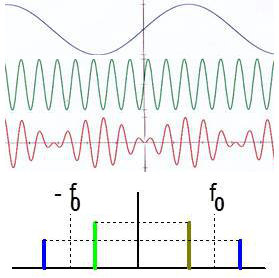 Un premier mouvement de grande période \(T_0\) donc de basse fréquence \(f_0(BF)\) et un deuxième mouvement de très faible période \(T_1\) donc de haute fréquence \(f_1(HF)\).
Un premier mouvement de grande période \(T_0\) donc de basse fréquence \(f_0(BF)\) et un deuxième mouvement de très faible période \(T_1\) donc de haute fréquence \(f_1(HF)\).
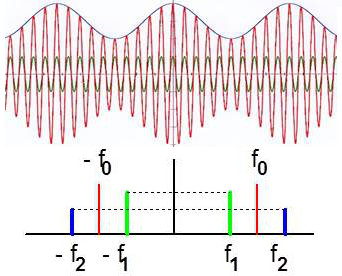
Le mouvement représenté à la figure ci-contre résulte de la multiplication des deux fonctions sinusoïdales du temps, chacune d’entre elles gardant la forme de sa nature spécifique.
On dit que le signal BF est porté par le signal HF. On dit encore que le signal HF est modulé par le signal BF.
Dans l’espace des fréquences (représentation spectrale), le spectre du signal résultant se compose de deux raies situées symétriquement par rapport à la fréquence \(f0\) dans les parties positive et négative de l’échelle des fréquences : \(f_2 - f_0 = f_0 - f_1\).
Le signal résultant oscille avec l’axe des abscisses comme support.
La raie de fréquence \(f_0\) est absente dans le spectre résultant. Cela tient au fait que le signal BF ne comporte pas de composante continue.
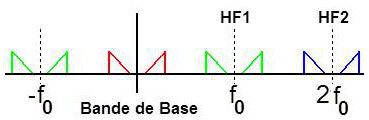 On peut ainsi considérer un signal BF plus complexe (c’est-à-dire composé d’une multitude de fréquences) porté par un signal sinusoïdal de fréquence \(f_0\) et sa représentation spectrale avec reproduction symétrique par rapport aux fréquences \(f_0\) et \(– f_0\) (avec ou sans raie effective) et leurs multiples.
On peut ainsi considérer un signal BF plus complexe (c’est-à-dire composé d’une multitude de fréquences) porté par un signal sinusoïdal de fréquence \(f_0\) et sa représentation spectrale avec reproduction symétrique par rapport aux fréquences \(f_0\) et \(– f_0\) (avec ou sans raie effective) et leurs multiples.
Le signal modulé a pour expression générale : \[s(t)=A~m(t)~\cos(2\pi~f_0~t)\]
Le signal modulant \(m(t)\) est le signal à transmettre et \(A\) est l’amplitude de la porteuse.
En désignant par \(M(f\)) le spectre du signal modulant en bande de base, le spectre du signal modulé sera : \[S(f)=\frac{A}{2}~M(f+f_0)+\frac{A}{2}~M(f-f_0)\]
On retient, comme le montre le schéma ci-dessus, que la bande de fréquences occupées par le signal modulé, et donc la bande nécessaire pour sa transmission, a une largeur double de celle du signal de départ.
La porteuse (qui correspondrait à une raie à la fréquence (\(\pm f_0\)) n’est pas présente dans le spectre. On a translaté le spectre en bande de base autour de cette fréquence porteuse.
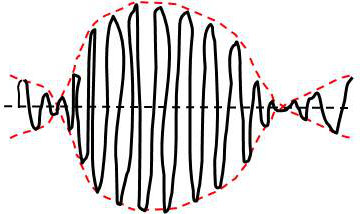 La forme du signal \(m(t)\) est quelconque. Le signal enveloppe présente une symétrie par rapport à l’axe des abscisses. L’enveloppe de \(s(t)\) s’annule en même temps que \(m(t)\).
La forme du signal \(m(t)\) est quelconque. Le signal enveloppe présente une symétrie par rapport à l’axe des abscisses. L’enveloppe de \(s(t)\) s’annule en même temps que \(m(t)\).
Dans le cas précédent, il s’agissait d’une forme sinusoïdale de part et d’autre de l’axe de la fonction porteuse.
Pour restituer en réception le signal d’information \(m(t)\), on a recours à une démodulation cohérente.
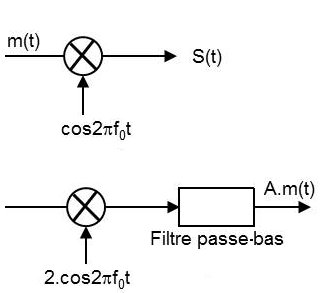 Mathématiquement, on obtient en sortie :
Mathématiquement, on obtient en sortie :
\[\begin{aligned} &s(t)~2\cos(2\pi~f_0~t)\\ =~&2~A~m(t)~\cos^2(2\pi~f_0~t)\\ =~&A~m(t)+A~m(t)~\cos(4\pi~f_0~t)\end{aligned}\]
Le deuxième terme est un terme HF qui peut être éliminé par filtrage passe-bas en laissant passer le signal BF porteur de l’information.
Le mot cohérente vient de ce que la connaissance précise de la fréquence et de la phase de la porteuse est requise. Imaginons en effet que le signal multiplicateur ne soit pas tout à fait en phase avec la porteuse. On réalise alors : \[s(t)~2~\cos(2\pi~f_0~t+\varphi)\]
C’est-à-dire, tous calculs faits :
\[\begin{aligned} &2A~m(t)~\cos(2\pi~f_0~t).\cos(2\pi~f_0~t+\varphi)\\ =~&A~m(t)~\cos(\varphi)+A~m(t)~\cos(4\pi~f_0~t+\varphi)\end{aligned}\]
Après filtrage passe–bas, le signal reçu est : \[A~m(t)~\cos(\varphi)\]
Il se produit donc, par rapport à la démodulation cohérente, une atténuation du signal démodulé, qui entraîne une dégradation réelle de la qualité de la transmission. Il est donc nécessaire de réaliser en réception des oscillateurs locaux suffisamment stables.
3. Modulation avec porteuse
 Le résultat aurait été légèrement différent en multipliant entre eux les deux signaux : \[s_0(t)=a_0~\cos(\omega_0~t)\quad;\quad s_1(t)=k+a_1~\cos(\omega_1~t)\]
Le résultat aurait été légèrement différent en multipliant entre eux les deux signaux : \[s_0(t)=a_0~\cos(\omega_0~t)\quad;\quad s_1(t)=k+a_1~\cos(\omega_1~t)\]
On a représenté figures ci-contre le signal résultant en fonction du temps et le spectre en fréquences.
On remarquera cette fois que si la constante \(k\) a une valeur positive assez grande, la résultante sera positive avec répartition symétrique de part et d’autre de l’axe de la sinusoïde porteuse.
On notera également la présence d’une raie à la fréquence porteuse dans le spectre résultant.
3.1. Remarque d’ordre physique
À partir de la partie positive de largeur B (physique) du spectre du signal BF à transmettre, il s’est crée d’autres spectres de largeur 2B. Nous verrons comment exploiter ou supprimer la présence de cette double bande engendrée par la modulation.
D’une manière générale, on écrira le signal modulé sous la forme : \[s(t)=A~\{1+k~m(t)\}~\cos(2\pi~f_0~t)\quad;\quad |k~m(t)|<1\]
La différence essentielle entre le signal DBAP et le signal DBSP est que l’enveloppe du signal DBAP ne s’annule jamais : en jouant sur le paramètre \(k\), on maintient strictement : \[-1~<~k~m(t)~<~+1\]
L’enveloppe de \(s(t)\) a exactement la forme du signal de départ \(m(t)\).
Si \(m(t)\) est un signal déterministe de spectre \(M(f)\), on a : \[S(f)=\frac{A}{2}~\delta(f+f_0)+\frac{A}{2}~\delta(f-f_0)+\frac{kA}{2}~M(f+f_0)+\frac{kA}{2}~M(f-f_0)\]
La largeur de bande du signal transmise est, comme pour la modulation DBSP, le double de celle du message.
On a également translaté le spectre en bande de base autour de la fréquence porteuse, mais ici, la fréquence porteuse a également été transmise.
La génération de ce signal DBAP peut se faire avec un modulateur DBSP qui fournit un signal auquel on ajoute une porteuse pure issue du même oscillateur.
On pourrait démoduler un signal DBA à l’aide d’un démodulateur cohérent, mais il y a plus simple avec le détecteur d’enveloppe :
3.2. Détection d’enveloppe
Pour un signal DBAP, l’enveloppe de la sinusoïde porteuse n’est pas une sinusoïde, mais une forme quelconque qui dépend du message BF émis. La symétrie du signal est cependant conservée, la forme du message se retrouvant en partie supérieure et en partie inférieure.
 On notera que la présence du terme \(k > 0\) a permis de maintenir l’enveloppe dans les ordonnées positives, ce qui rend possible sa détection avec un détecteur d’enveloppe classique.
On notera que la présence du terme \(k > 0\) a permis de maintenir l’enveloppe dans les ordonnées positives, ce qui rend possible sa détection avec un détecteur d’enveloppe classique.
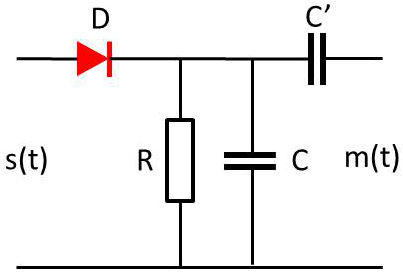
La diode ne laisse passer que les arches positives de \(s(t)\).
L’ensemble RC constitue un filtre passe bas restituant l’enveloppe de \(s(t)\) par élimination des HF (signal porteur).
La capacité C’ sert à supprimer la composante continue de façon à retrouver \(m(t)\).

