1. Considérations physiques
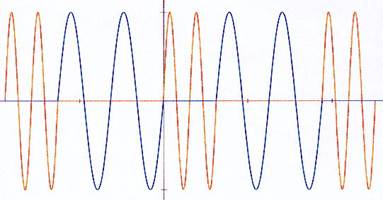La figure ci-contre montre une modulation en fréquence.
On retrouve une partie de sinusoïde à une fréquence haute (partie serrée) et une partie de sinusoïde à une fréquence basse (partie large) : le système de l’accordéon.
Cet exemple peut correspondre au cas de la transmission d’une série de bits \([1 0 1 0 1]\) : au symbole 1 est associé une sinusoïde de fréquence \(f_1\) et au symbole 0 est associé une fréquence \(f_2\).
2. Définition de la modulation
Le signal a pour expression : \[s(t)=A~\cos\{2\pi[f_0+f(t)]~t\} =A~\cos\{2\pi~f_0~t+\varphi(t)\}\]
\(\varphi(t)\) contient l’information utile \(m(t)\).
On définit :
– la phase instantanée : \[\theta(t)=2\pi~f_0~t+\varphi(t)\]
– la fréquence instantanée : \[F(t)=\frac{1}{2\pi}~\frac{d\theta(t)}{dt}=f_0+\frac{1}{2\pi}~\frac{d\varphi(t)}{dt}\]
Pour réaliser une modulation de fréquence, il faut transformer les variations du signal modulant \(m(t)\) en variation de la fréquence instantanée \(F(t)\) du signal \(s(t)\).
Cette transformation est en pratique toujours linéaire, du type : \[F(t)=f_0+k~m(t)\quad;\quad k\text{ en Hz/V}\]
On obtient alors : \[\theta(t)=2\pi\int_0^t F(t)~dt=2\pi~f_0~t+2\pi~k\int_0^tm(u)~du\]
Le signal modulé en fréquence par un message \(m(t)\) s’écrit : \[s(t)=A~\cos\big\{2\pi~f_0~t+2\pi~k\int_0^tm(u)~du\big\}\]
3. Analyse spectrale du signal MF
3.1. Cas d’un signal modulant sinusoïdal
Considérons le cas simple où \(m(t)\) est un signal modulant sinusoïdal :
\[\begin{aligned} m(t)&=A_m~\cos(2\pi~f_m~t)\\ F(t)&=f_0+k~m(t)=f_0+A_m~\cos(2\pi~f_m~t)\end{aligned}\]
La variation est sinusoïdale dans un intervalle : \[[f_0-\Delta f,~f_0-\Delta f]\quad;\quad\Delta f=k~A_m\quad\text{excursion en fréquence}\]
Pour la phase instantanée : \[\theta(t)=2\pi\int_0^tF(u)~du=2\pi~f_0~t+\frac{k~A_m}{f_m}~\sin(2\pi~f_m~t)\]
On définit un indice de modulation (sans dimension) : \[\beta=\frac{k~A_m}{f_m}=\frac{\Delta~f_m}{f_m}\]
D’où l’expression du signal modulé : \[s(t)=A~\cos\{2\pi~f_0~t+\beta~\sin(2\pi~f_m~t)\}\]
On démontre que : \[s(t)=A\sum_{n=-\infty}^{n=+\infty}J_n(\beta)~\cos\{2\pi(f_0+n~f_m~t)\}\]
\(J_n(\beta)\) est la fonction de Bessel de première espèce d’ordre \(n\).
En passant à la transformation de Fourier : \[S(f)=\frac{A}{2}\sum_{n=-\infty}^{n=+\infty}J_n(\beta)~\{\delta(f-f_0-n~f_m)+\delta(f+f_0+n~f_m)\]
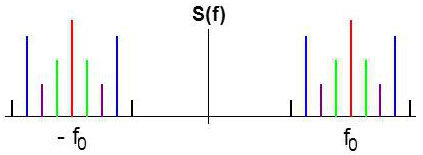Le spectre d’une onde modulée en fréquence se compose d’une fréquence porteuse, d’une infinité de bandes latérales, situées de part et d’autre de la porteuse, séparées par des intervalles égaux \(f_m\) : \[\left. \begin{aligned} &\text{Amplitudes~:} &&\frac{A}{2}~J_n(\beta) \\ &\text{Abscisses~:} &&(\pm f_0 \pm n~f_m) \end{aligned}\right\} \quad n\in[-\infty~,~+\infty]\]
Le nombre de raies contenues dans le spectre est théoriquement infini, mais leur amplitude décroît pour \(n\) grand jusqu’à devenir négligeable. En pratique, le signal MF peut être considéré comme un signal de largeur de bande limitée.
En désignant par \(N\) le nombre de paires de raies d’amplitude significative, la largeur de bande utile du signal MF modulé par un signal sinusoïdal de fréquence \(f_m\) est donnée par \(B = 2~N~f_m\).
On garde, pour la mesure de \(N\), les raies qui contiennent au moins 99 % de la puissance totale du signal MF.
Compte tenu du fait que (propriétés des fonctions de Bessel): \[J_{-n}(\beta)=(-1)^n~J_n(\beta)\quad;\quad\sum_{n=-\infty}^{+\infty}J_n^2(\beta)=1\]
on a pour l’expression de la puissance (train d’impulsions) : \[P=\frac{A^2}{2}~\big\{2J_0^2(\beta)+2J_1^2(\beta)+2J_2^2(\beta)+\dots\big\}=\frac{A^2}{2}\]
Le nombre \(N\) de raies significatives est donc tel que : \[J_0^2(\beta)+2~J_1^2(\beta)+2~J_2^2(\beta)+\dots~\approx~0,99\]
Ce nombre \(N\) vérifie la relation : \(N=\beta +1\)
La largeur de bande utile d’un signal MF (bande de Carson) modulé par une sinusoïde de fréquence \(f_m\) avec un indice de modulation \(\beta\) est donc : \[B=2~(\beta~f_m+1)=2~(\Delta f+f_m)\]
3.2. Cas d’un signal modulant quelconque
Si \(m(t)\) est un signal modulant quelconque, le calcul exact de la forme du spectre ne saurait être entrepris (sauf dans quelques cas très particuliers où \(\beta\) est soit très faible, soit très grand). On peut cependant définir un indice de modulation généralisé :
\[\begin{aligned} \beta&=\frac{\delta f}{b} &&\text{largeur de bande du modulant}\\ \Delta f&=k~|m(t)|_{max} &&\text{excursion maximale de la fréquence instantanée}\end{aligned}\]
La largeur utile de ce signal MF est alors : \[B=2~(\Delta f+b)=2~(\beta +1)~b\]
On remarque que :
-
pour un indice de modulation grand : \(B\approx 2~\beta~b\approx 2~\Delta f\).
La largeur de bande du signal MF ne dépend plus que de l’amplitude du signal modulant.
-
pour un indice de modulation faible : \(B\approx 2~b\).
La largeur de bande du signal MF est pratiquement égale au double de la largeur de bande du signal modulant comme en MA.
La largeur de bande du signal MF est pratiquement égale au double de la largeur de bande du signal modulant comme en MA.
4. Génération des signaux MF
Générer des signaux MF consiste à transformer des variations de tension en variations de fréquence. \[f(v)=f_0+k~v \quad;\quad k \text{ en Hz/V}\]
Pour une tension d’entrée nulle \((v = 0)\), la fréquence délivrée par le modulateur est égale à la fréquence porteuse \(f_0\).
\(k\) est appelée sensibilité du modulateur. Ce coefficient mesure la déviation de fréquence \(\Delta f\) produite par une variation \(\Delta v\) de tension en entrée. On l’appelle aussi la pente du modulateur.
Il n’est pas toujours facile de générer un signal d’amplitude parfaitement constante comme se doit de l’être un signal MF. Un modulateur fabriquera toujours un signal présentant des variations d’amplitude parasites, mais celles-ci pourront être éliminées à l’aide d’un limiteur qui écrête fortement le signal sans changer sa fréquence.
La fréquence d’un oscillateur est déterminée par la valeur des paramètres des composants qui le constituent. Si l’on sait faire varier la valeur de ces paramètres en fonction d’un signal externe, par exemple une tension de commande \(v\), on aura réalisé un oscillateur modulable en fréquence appelé oscillateur commandé en tension.
On peut par exemple utiliser une diode Varicap, composant dont la capacité varie en fonction de la tension qui lui est appliquée.
5. Démodulation des signaux MF
Une des méthodes utilisées pour démoduler un signal MF est la démodulation par discriminateur. Le signal MF a pour expression : \[s(t)=A~\cos\big\{2\pi~f_0~t+2\pi~k\int_0^tm(u)~du\big\}\]
D’où, en dérivant : \[\frac{d}{dt}s(t)=-A~\big\{2\pi~f_0+2\pi~k~m(t)\big\}\cdot\sin\big\{2\pi~f_0~t+2\pi~k\int_0^tm(u)du\big\}\]
Ce signal est encore un signal modulé en fréquence, mais son enveloppe est devenue une fonction linéaire du signal modulant \(m(t\)).
Pour récupérer ce dernier, il suffit donc de mesurer à tout instant l’enveloppe du signal dérivée.
Pour démoduler, il faut donc utiliser un filtre dérivateur (dont la fonction de transfert présente un gain linéaire en fonction de la fréquence sur la bande B du signal modulé), puis un détecteur d’enveloppe du même type que celui utilisé pour la démodulation des signaux DBAP.
Ce démodulateur étant sensible aux variations d’amplitude parasites du signal MF, il faut faire précéder le discriminateur d’un limiteur.
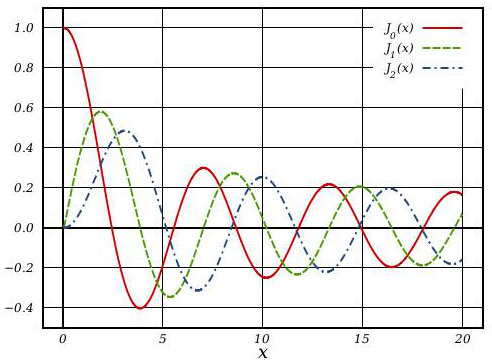
6. Appendice. Fonctions de Bessel \(J_n(\beta)\)
\[\begin{aligned} n/\beta&&1&&2&&3 &&4 &&5 &&6 &&7 &&8 &&9 &&10\\ 0&&.765&&.224&&-.260&&-.397&&-.178&&.150 &&.300 &&.172 &&-.090&&-.246\\ 1&&.440&&.577&&.339 &&-.066&&-.328&&-.277&&-.004&&.234 &&.245 &&.043\\ 2&&.115&&.353&&.486 &&.364 &&.046 &&-.243&&-.301&&-.113&&.145 &&.254\\ 3&&.019&&.129&&.309 &&.430 &&.364 &&.115 &&-.167&&-.291&&-.181&&.058\\ 4&&.002&&.034&&.132 &&.281 &&.391 &&.357 &&.158 &&-.105&&-.265&&-.219\\ 5&& &&.007&&.043 &&.132 &&.261 &&.362 &&.348 &&.185 &&-.055&&-.234\\ 6&& &&.001&&.011 &&.049 &&.131 &&.246 &&.339 &&.327 &&.204 &&-.014\\ 7&& && &&.002 &&.016 &&.054 &&.129 &&.233 &&.320 &&.327 &&.216\\ 8&& && && &&.004 &&.018 &&.056 &&.128 &&.223 &&.305 &&.318\\ 9&& && && && &&.005 &&.022 &&.059 &&.126 &&.215 &&.292\\ 10&& && && && &&.001 &&.007 &&.023 &&.060 &&.125 &&.207\\ 11&& && && && && &&.002 &&.008 &&.025 &&.062 &&.0123\\ 12&& && && && && && &&.003 &&.009 &&.027 &&.064\\ 13&& && && && && && && &&.003 &&.011 &&.003\\ 14&& && && && && && && &&.001 &&.004 &&.012\\ 15&& && && && && && && && &&.001 &&.004\\ 16&& && && && && && && && && &&0.01\end{aligned}\]
