1. Circuits à constantes réparties
Tout élément d’un conducteur présente une capacité propre et une self propre. Cet effet est particulièrement important :
-
dans les fils longs constituant les lignes,
-
dans les fils ou rubans courts en haute fréquence,
les capacités ou selfs parasites présentant alors des admittances ou impédances notables.
2. Ligne homogène. Équation des télégraphistes
Une ligne homogène est constituée par deux circuits filiformes, disposés côte à côte, le long desquels la tension \(V\) et l’intensité \(I\) varient selon la loi :
\[\begin{aligned} dV&=-\Big(r+\Lambda~\frac{\partial}{\partial t}\Big)I~dx \\ dI&=-\Big(g+\Gamma~\frac{\partial}{\partial t}\Big)V~dx\end{aligned}\]
-
\(r\) : résistance de la ligne par unité de longueur
-
\(\Lambda\) : self de la ligne par unité de longueur
-
\(g\) : conductance de la ligne par unité de longueur
-
\(\Gamma\) : capacité de la ligne par unité de longueur
Exemples : deux fils parallèles ; deux cylindres parallèles.
On en déduit que \(V\) et \(I\) satisfont à l’équation : \[\frac{\partial^2Y}{\partial x^2}=\Big(r+\Lambda\frac{\partial}{\partial t}\Big)\Big(g+\Gamma\frac{\partial}{\partial t}\Big)Y\]
C’est l’équation des télégraphistes dont une solution particulière est :
\[\begin{aligned} Y&=\Lambda(\omega)~\exp(j~\omega~t\pm\gamma~x)\\ \gamma&=\pm\sqrt{(r+j~\omega~\Lambda)~(g+j~\omega~\Gamma)}\end{aligned}\]
C’est en général une fonction complexe : \[\gamma=\alpha(\omega)+j~\beta(\omega)\]
D’où l’expression de la solution : \[Y_{\pm}=\Lambda(\omega)~\exp\{j~(\omega~t\mp\beta~x)\}~exp\{\mp\alpha~x\}\]
Revenant aux équations de définition : \[\frac{V_+}{I_+}=-\frac{V_-}{I_-}=\sqrt{\frac{r+j~\omega~\Lambda}{g+j~\omega~\Gamma}}=Z_c^+\]
La solution du type \(Y_+\) correspond à un signal circulant dans le sens des \(x\) croissant, avec une vitesse de phase : \[v=\frac{\omega}{\beta}\]
généralement fonction de \(\omega\) et une atténuation de constante \(\alpha\) généralement fonction de \(\omega\). Le signal subit donc en général une déformation en phase et en amplitude.
La solution générale est obtenue en combinant les composantes de Fourier \(Y(\omega)\) et en tenant compte des conditions aux limites :
\[\begin{aligned} Y&=(Y_+)+(Y_-)\\ Y_+&=\int_{-\infty}^{+\infty}f_+(\omega)~\exp\{j~(\omega~t-\beta~x)\}~\exp\{-\alpha~x\}~d\omega\\ Y_-&=\int_{-\infty}^{+\infty}f_-(\omega)~\exp\{j~(\omega~t+\beta~x)\}~\exp\{\alpha~x\}~d\omega\end{aligned}\]
3. Exemple: ligne sans réflexion attaquée à l’entrée
C’est le cas d’une ligne infinie, car \(I\) et \(V\) tendent vers zéro quelle que soit l’impédance terminale.
Seules conviennent les solutions \(Y_+\).
On décompose \(Y_0=Y_{(x=0)}\) en intégrale de Fourier :
\[\begin{aligned} Y_0&=\int_{-\infty}^{+_\infty}y(\omega)~\exp(j~\omega~t)~d\omega\\ y(\omega)&=\frac{1}{2\pi}\int_{-\infty}^{+\infty}Y_0~\exp(-j~\omega~t)~dt\end{aligned}\]
Il vient : \[Y=\int_{-\infty}^{+\infty}y(\omega)~\exp\{j~(\omega~t-\beta~x)\}~\exp\{-\alpha~x\})~d\omega\]
Pour une ligne sans perte (\(r=g=0\)) : \[\frac{\partial^2Y}{\partial x^2}=\Lambda~\Gamma~\frac{\partial^2 x}{\partial t^2}\]
Il vient : \[Y=f\Big(t-\frac{x}{v}\Big)+g\Big(t+\frac{x}{v}\Big)\qquad\text{avec~:}\quad v=\frac{1}{\sqrt{\Lambda~\Gamma}}\]
Il y a propagation sans déformation.
Si la ligne est attaquée en \(x=0\) et si le signal se propage suivant les \(x>0\) :
-
\(f(t-x/v)\) correspond à la somme des signaux émis depuis \(x=0\) ;
-
\(g(t+x/v)\) correspond à la somme des signaux réfléchis à l’extrémité.
Notons que, d’une manière générale, la réflexion s’effectue avec changement de signe :
-
pour \(V\) si \(Z_{ter}=0\),
-
pour \(I\) si \(Z_{ter}=\infty\),
de manière à annuler \(V\) ou \(I\).
Le signal réfléchi est nul si la ligne est fermée sur une impédance (dite caractéristique) : \[Z_c=\sqrt{\frac{r+j~\omega~\Lambda}{g+j~\omega~\Gamma}}\]
\(Z_c=V_+/V_-\) est alors satisfaite en bout de ligne.
\(Z_c\) est indépendante de la fréquence si \(r/g=\Lambda/\Gamma\).
Dans une ligne sans perte, \(r\) et \(g\) sont indépendants de \(\omega\).
4. La ligne homogène comme chaîne de quadripôles
4.1. Impédance caractéristique
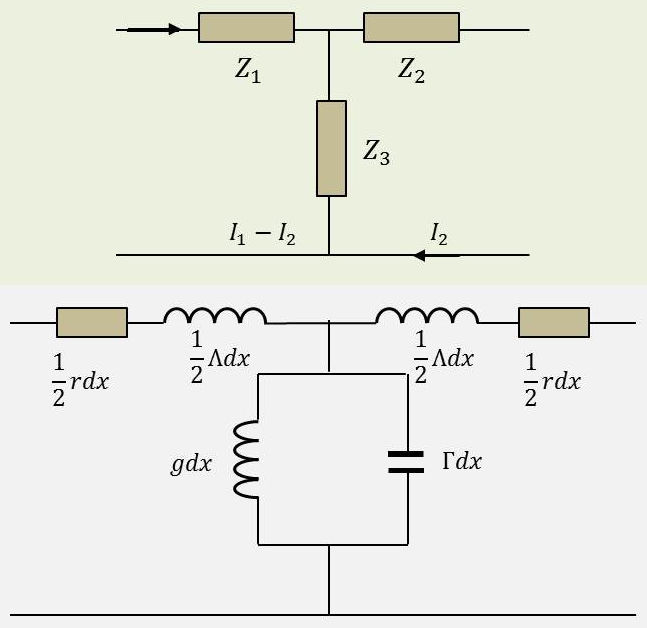Les équations de la ligne sont satisfaites par la cellule en \(T\) (symétrique) représentée ci-contre :
\[\begin{aligned} Z_1&=\frac{1}{2}~(r+j~\omega~\Lambda)~dx=Z_2\\ Z_3&=\frac{1}{(g+j~\omega~\Gamma)~dx}\end{aligned}\]
La ligne peut donc être considérée comme une suite de tels quadripôles.
Les matrices impédance et de transfert sont données par les relations suivantes :
1) Impédance : matrice [\(z\)] : \[\begin{pmatrix} V_1\\ V_2 \end{pmatrix} = \begin{pmatrix} Z_1+Z_3&-Z_3\\ Z_3&-(Z_1+Z_3) \end{pmatrix} ~ \begin{pmatrix} I_1\\ I_2 \end{pmatrix}\]
2) Transfert : matrice [\(\gamma\)] : \[\begin{pmatrix} V_2\\ I_2 \end{pmatrix} = \begin{pmatrix} 1+\cfrac{Z_1}{Z_3} &~~-2~Z_1-\cfrac{Z_1^2}{Z_3}\\ -\cfrac{1}{Z_3} &~~1+\cfrac{Z_1}{Z_3} \end{pmatrix} ~ \begin{pmatrix} V_1\\ I_1 \end{pmatrix}\]
En se rapportant à la théorie des quadripôles étudiée précédemment, on démontre que l’impédance caractéristique \(Z_c\) a pour expression : \[Z_c=\sqrt{\frac{r+j~\omega~\Lambda}{g+j~\omega~\Gamma}}\]
4.2. Remarques
-
Une ligne fermée sur \(Z_c\) a une impédance d’entrée égale à \(Z_c\).
Il en est encore ainsi si la ligne est infinie.
-
L’impédance d’entrée d’une ligne infinie à pertes est indépendante de l’impédance terminale (car \(V=0\) et \(I=0\)).
L’impédance d’entrée d’une ligne infinie est donc \(Z_c\).
Réciproquement, une ligne fermée sur \(Z_c\) se comporte comme une ligne infinie étant en général fonction de \(\omega\).
Il n’en est en général ainsi que pour un signal monochromatique.
-
Dans les cas où \(r\ll\omega~\Lambda\) et \(g\ll\omega~\Gamma\) : \[Z_c\approx\sqrt{\frac{\Lambda}{\Gamma}}\quad;\quad\frac{\gamma}{j~\omega}\approx-\sqrt{\Lambda~\Gamma}\]
Ces deux quantités sont réelles et indépendantes de \(\omega\).
