1. Propagation d’un signal BF sur une ligne infinie peu selfique

On suppose les composantes de Fourier du signal bornées supérieurement et inférieurement par \(\omega_{sup}\) et \(\omega_{inf}\) telles que : \[\omega_{sup}\Lambda~\ll~r\quad;\quad\omega_{inf}~\gg~g\]

Quelques valeurs courantes en laboratoire :

\[\begin{aligned} &r\approx 10^{-1}~\rm \Omega~m^{-1} &&\Gamma\approx 10^{-10}~\rm F~m^{-1}\\ &g\approx 10^{-10}~\rm M\Omega &&\Lambda=10^{-7}~\rm H~m^{-1}\end{aligned}\]

Pour de telles caractéristiques : \[{\rm 1~s^{-1}}~\ll~\omega_{inf}~\leq~\omega~\leq~\omega_{sup}~\ll~10^6~\rm s^{-1}\]

La condition est donc vérifiée pour les sons audibles.

Il vient : \[Z_c=\sqrt{\frac{r}{j~\omega~\Gamma}}\]

Pour une ligne infinie : \[\gamma=\sqrt{j~\omega~\Gamma~r}=(1+j)~\sqrt{\frac{r~\Gamma~\omega}{2}}\]

Car on peut écrire : \[\sqrt{j}=\exp\Big(j~\frac{\pi}{4}\Big)=\frac{1+j}{\sqrt{2}}\]

Pour \(\omega=10^4\) : \[|Z_c|~\approx~3000~\Omega\quad;\quad\gamma=(1+j)~\sqrt{5}\times 10^{-4}\]

Comme \(\gamma=\alpha+j~\beta\) : \[V=\frac{\omega}{\alpha}=\frac{10^8}{\sqrt{5}}~\rm m~s^{-1}\qquad\text{vitesse de phase}\]

Et pour l’atténuation (en \(l/c)\) : \[\frac{1}{\sqrt{5}\times10^{-4}}=\frac{10}{\sqrt{5}}~\rm km\approx 4,5~km\]

Note : On peut augmenter la portée en diminuant \(\Gamma\), donc en écartant les fils (exemple des fils téléphoniques, à présent anciens).

2. Propagation d’un signal sur une ligne selfique peu résistante

On suppose que : \[r~\ll~\omega\Lambda\quad;\quad g~\lll~\omega~\Gamma\]

Il vient :

\[\begin{aligned} Z_c~&\approx~\sqrt{\frac{\Lambda}{\Gamma}}\\ \gamma~&\approx~\sqrt{j~\omega~\Gamma(r+j~\omega~\Lambda)}~\approx~j~\omega~\sqrt{\Lambda~\Gamma}~(1+\frac{r}{2j~\omega~\Lambda})\end{aligned}\]

Par suite :

\[\begin{aligned} V~&\approx~\frac{1}{\sqrt{\Lambda\Gamma}} &&\text{sensiblement indépendant de la pulsation}\\ \alpha~&\approx~\frac{r}{2}~\sqrt{\frac{\Gamma}{\Lambda}}~\approx~\frac{r}{2~Z_c} &&\text{également constant, à l'effet de peau près}\end{aligned}\]

On peut donc raisonner sur une ligne finie, supposée fermée sur son impédance caractéristique.

Remarques

1. En HF, (\(\omega\gg r/\Lambda\)), \(Z_c\) et \(V\) sont indépendants de \(\omega\). Toutefois, pour l’atténuation, il faut tenir compte de l’effet de peau.

2. On peut accroître la portée de la ligne en augmentant \(\Lambda\), ce qui diminue en même temps la vitesse de propagation et abaisse la borne inférieure des fréquences où l’approximation est valide. On intercalera par exemple des bobines de self d’une manière régulière (pupinisation). Simultanément, \(Z_c\) est augmentée, ce qui peut présenter des inconvénients.

3. Propagation d’une onde HF dans un coaxial

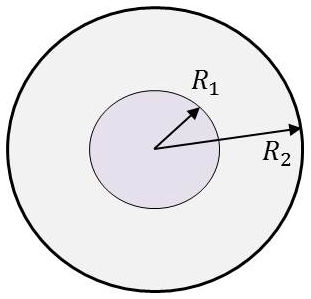Dans un coaxail, on peut calculer \(\Lambda\) et \(\Gamma\), d’où \(Z_c\) et \(V\).

D’après l’électrostatique : \[\Gamma=\frac{2\pi~\varepsilon}{\ln\cfrac{R_2}{R_1}}\]

Nous pouvons obtenir l’expression de la self à l’aide de l’énergie magnétique emmagasinée dans l’espace entre conducteurs (en supposant donc que par effet de peau le courant intérieur est superficiel et que \(H\) est nul dans le cylindre intérieur) : \[\frac{1}{2}~\Lambda~I^2=\frac{1}{2}\int_{R1}^{R2} dS=\frac{1}{2}~\frac{\mu~I^2}{4\pi^2}\int_{R1}^{R2}~\frac{2\pi ~r}{r^2}~dr\]

Tous calculs faits : \[\Lambda=\frac{\mu}{2\pi}~\ln\frac{R_2}{R_1}\]

Pour information : \[\mu_0~\varepsilon_0~c^2=1\quad;\quad\sqrt{\frac{\mu_0}{\varepsilon_0}}=376~\Omega\]

On construit couramment des lignes de \(Z_c=50~\Omega\).

4. Réflexion à l’extrémité d’une ligne (prise comme origine)

Pour une composante monochromatique, on sait que la fonction \(Y\) est une combinaison linéaire de solutions en \(\exp(j~\omega~t\mp\gamma~x)\).

avec : \[\gamma=\alpha+j~\beta=\sqrt{(r+j~\omega~\Lambda)~(g+j~\omega~\Gamma)}\]

Soit :

\[\begin{aligned} v_x&=V_{0+}\exp(j~\omega~t-\gamma~x)+V_{0-}\exp(j~\omega~t+\gamma~x)\\ i_x&=I_{0+}\exp(j~\omega~t-\gamma~x)+I_{0-}\exp(j~\omega~t+\gamma~x)\end{aligned}\]

Avec : \[\frac{V_{0+}}{I_{0+}}=-\frac{V_{0-}}{I_{0-}}=Z_c\qquad\text{donc:}\quad\frac{V_{0-}}{V_{0+}}=-\frac{I_{0-}}{I_{0+}}\]

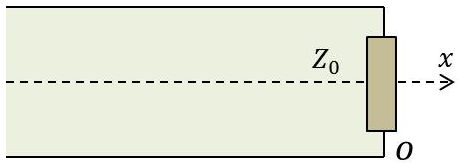Chacun des termes est une onde atténuée en \(\exp(\alpha~|x|)\) et se propageant à la vitesse de \(\omega/\beta\) :

• dans le sens \((+)\) pour l’onde \((+)\),

• dans le sens \((-)\) pour l’onde \((-)\).

En \(O\) (\(x=0\)), nous aurons : \[\frac{V_0}{I_0}=Z_0=\frac{V_{0+}+V_{0-}}{I_{0+}+I_{0-}}=Z_c~\frac{I_{0+}-I_{0-}}{I_{0+}+I_{0-}}\]

Par définition, on pose pour le coefficient de réflexion en O est : \[\rho_0=\frac{V_{0-}}{V_{0+}}=-\frac{I_{0-}}{I_{0+}}\]

Il vient : \[Z_0=Z_c~\frac{1+\rho_0}{1-\rho_0}\quad\Rightarrow\quad\rho_0=\frac{Z_0-Z_c}{Z_0+Z_c}\]

On remarque que :

\[\begin{aligned} &\rho_0=0~\text{si}~Z_0=Z_c~: \text{ligne fermée sur son impédance caractéristique}\\ &\rho_0=1~\text{si}~Z_0=\infty~: \text{réflexion avec changement de signe pour }I\\ &\rho_0=-1~\text{si}~Z_0=0~: \text{réflexion avec changement de signe pour }V\end{aligned}\]

Nota

Supposons :

• \(Z_c=0\) (cas en particulier de la ligne sans perte) ;

• \(Z_0\) imaginaire pure soit \(Z_0=jY_0\),

il vient : \[\rho_0=\frac{j~Y_0-|Z_c|}{j~Y_0+|Z_c|}\quad;\quad\rho^*_0=\frac{-j~Y_0-|Z_c|}{-j~Y_0+|Z_c|}\]

On a alors : \[\rho_0~\rho_0^*=1\quad;\quad|\rho_0|=1\quad;\quad\rho_0=\exp(j~\varphi)\]

Il y a réflexion avec conservation de l’amplitude, mais avec déphasage.