La définition rigoureuse de l'oscillateur est celle d'un système qui évolue de part et d'autre d'un équilibre stable. Tout d'abord son existence mathématique. Revenant à l'époque de nos premiers calculs de dérivées (premières et secondes), en particulier celles des fonctions circulaires sinus et cosinus, chacune d'entre elles redonnant l'autre, au coefficient près et au signe près.
Ainsi, posant : \(x(t)=a\sin(\omega t) \), on obtient par dérivations successives : \(x''+\omega^2x=0 \) qui est l'équation de l'oscillateur idéal de pulsation \(\omega\), dit harmonique.
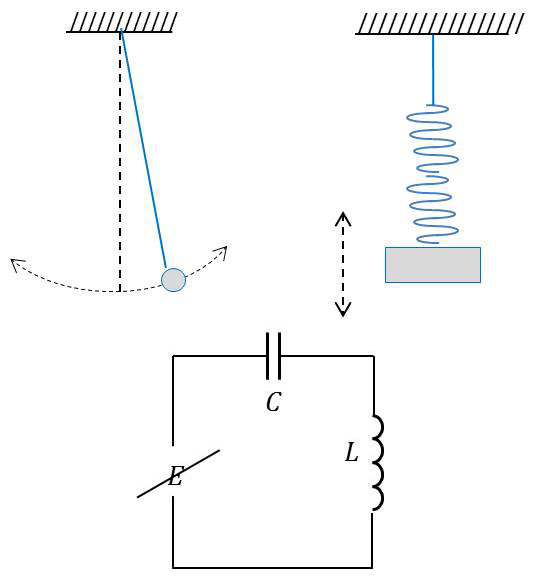Pour la physique et pour mémoire, la découverte des deux premiers oscillateurs mécaniques élémentaires (hypothèse des petits déplacements et sans perte d'énergie) :
- le pendule simple filaire
\(\alpha''+(g/l)~\alpha=0\quad;\quad\text{période}~T=2~\pi/\omega=2~\pi~\sqrt{m/k}\) - le pendule simple à ressort
\(y''+(k/m)~y=0\quad;\quad\text{période}~T=2~\pi/\omega=2~\pi~\sqrt{l/g}\) - et puis, peu après, l'oscillateur électrique (sans résistance)
\(u''+(1/L~C)~u=0\quad;\quad\text{période}~T=2~\pi/\omega=2~\pi~\sqrt{L~C}\)
u(t) désignant la tension aux bornes de C, la tension E appliquée à l'entrée ayant été supprimée après initialisation du processus
En réalité, les problèmes réels d'oscillateurs, très présents un peu partout dans la nature même quantifiée, ne se présentent pas le plus souvent de manière aussi simple quand il faut les expliquer, les associer, ni aussi idéale...
